Chào mừng bạn đến với bài học về lý thuyết Đường thẳng và mặt phẳng song song, một trong những chủ đề quan trọng nhất của chương trình Hình học không gian lớp 11 Kết nối tri thức.
Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản về điều kiện song song của đường thẳng và mặt phẳng, các tính chất và định lý liên quan, cùng với các ví dụ minh họa cụ thể.
1. Đường thẳng song song với mặt phẳng
1. Đường thẳng song song với mặt phẳng
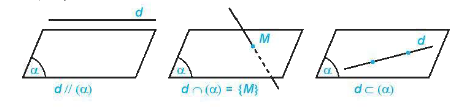
Cho đường thẳng d và mặt phẳng \(\left( \alpha \right)\). Nếu d và \(\left( \alpha \right)\) không có điểm chung thì ta nói d song song với \(\left( \alpha \right)\) hay \(\left( \alpha \right)\)song song với d. Kí hiệu là \(d//\left( \alpha \right)\)hay \(\left( \alpha \right)//d\).
*Nhận xét:
Nếu d và \(\left( \alpha \right)\) có một điểm chung duy nhất thì ta nói d và \(\left( \alpha \right)\) cắt nhau tại M. Kí hiệu \(d \cap \left( \alpha \right) = M\)hay \(d \cap \left( \alpha \right) = \left\{ M \right\}\).
Nếu d và \(\left( \alpha \right)\) có nhiều hơn 1 điểm chung thì ta nói d nằm trong \(\left( \alpha \right)\) hay \(\left( \alpha \right)\) chứa d. Kí hiệu \(d \subset \left( \alpha \right)\)hay \(\left( \alpha \right) \supset d\).
2. Điều kiện và tính chất của đường thẳng song song với mặt phẳng
Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì ta nói \(a//\left( P \right)\).
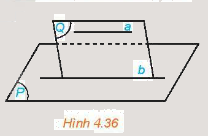
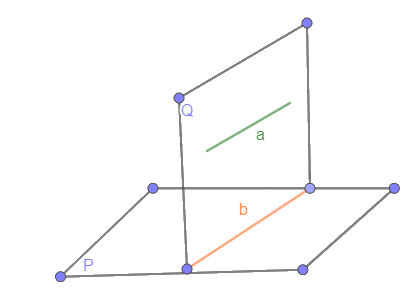
Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì b//a.
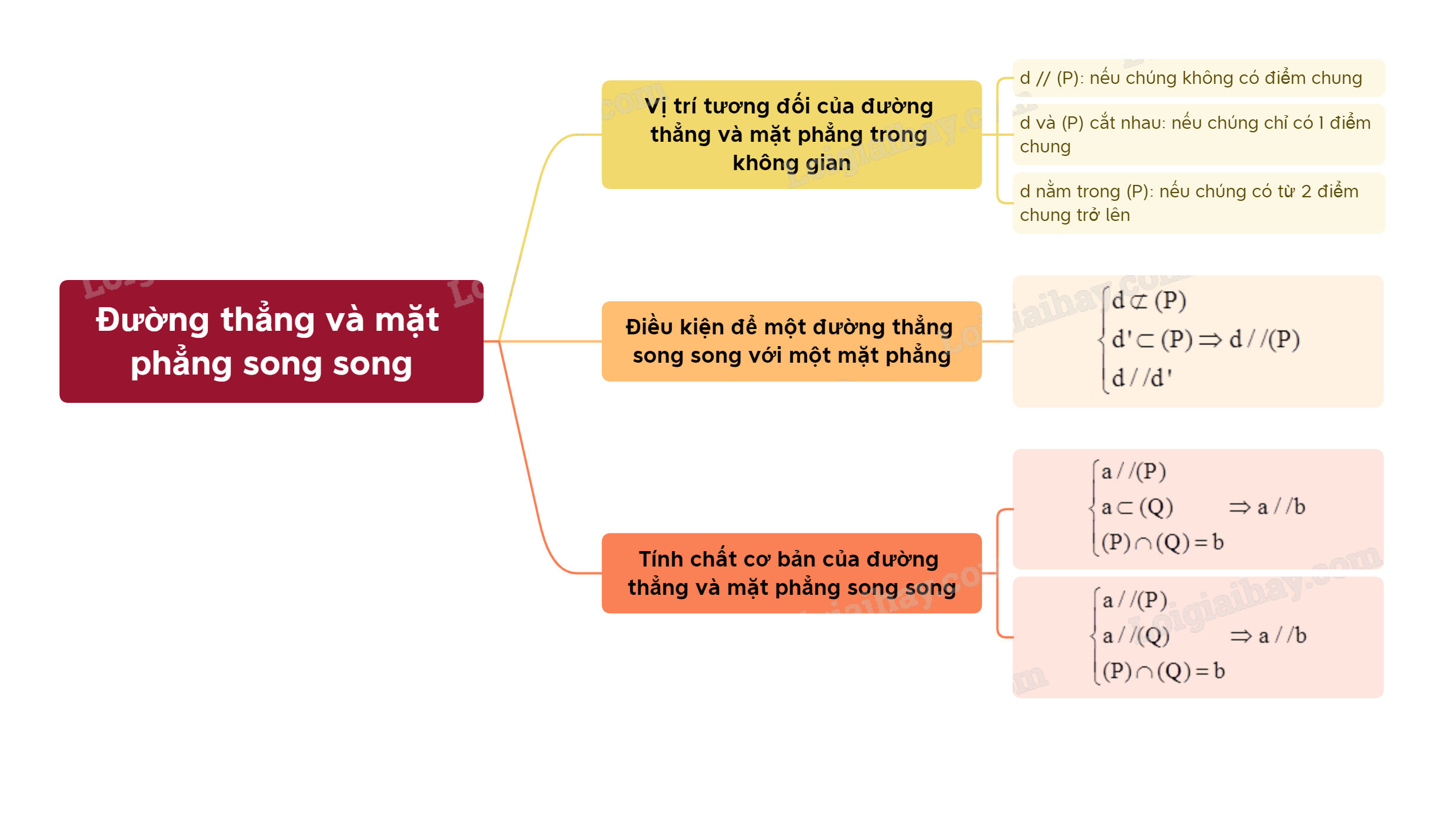
Chương trình Hình học không gian lớp 11 đóng vai trò quan trọng trong việc phát triển tư duy không gian và khả năng giải quyết vấn đề của học sinh. Trong đó, kiến thức về đường thẳng và mặt phẳng song song là nền tảng để hiểu và vận dụng các khái niệm phức tạp hơn trong các chương sau.
1. Đường thẳng song song: Hai đường thẳng được gọi là song song khi chúng không có điểm chung và nằm trong cùng một mặt phẳng.
2. Mặt phẳng song song: Hai mặt phẳng được gọi là song song khi chúng không có điểm chung.
3. Đường thẳng song song với mặt phẳng: Một đường thẳng được gọi là song song với một mặt phẳng khi nó không có điểm chung với mặt phẳng đó.
1. Điều kiện song song của hai đường thẳng:
2. Điều kiện song song của đường thẳng và mặt phẳng:
3. Điều kiện song song của hai mặt phẳng:
1. Tính chất:
2. Định lý:
Định lý về đường thẳng song song với mặt phẳng và các mặt phẳng song song với nhau là những công cụ quan trọng để chứng minh các bài toán hình học không gian.
Để hiểu rõ hơn về lý thuyết, chúng ta hãy xem xét một số bài tập vận dụng:
Ngoài những kiến thức cơ bản trên, bạn có thể tìm hiểu thêm về:
Lý thuyết Đường thẳng và mặt phẳng song song là một phần quan trọng của chương trình Hình học không gian lớp 11. Việc nắm vững kiến thức này sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và tự tin hơn. Hãy luyện tập thường xuyên và áp dụng các kiến thức đã học vào thực tế để đạt được kết quả tốt nhất.
| Khái niệm | Định nghĩa |
|---|---|
| Đường thẳng song song | Không có điểm chung và nằm trong cùng một mặt phẳng |
| Mặt phẳng song song | Không có điểm chung |
| Đường thẳng song song với mặt phẳng | Không có điểm chung với mặt phẳng |
| Bảng tóm tắt các khái niệm cơ bản | |