Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 89, 90, 91 sách giáo khoa Toán 11 tập 1 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
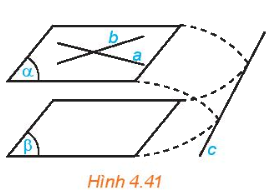
Cho mặt phẳng (left( alpha right)) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (left( beta right)) (H.4.41) Nếu (left( alpha right)) và (left( beta right)) cắt nhau theo giao tuyến c thì hai đường thẳng a và c có song song với nhau hay không, hai đường thẳng b và c có song song với nhau hay không? Hãy rút ra kết luận sau khi trả lời các câu hỏi trên.
Video hướng dẫn giải
Cho mặt phẳng \(\left( \alpha \right)\)chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng \(\left( \beta \right)\) (H.4.41)
Nếu \(\left( \alpha \right)\) và \(\left( \beta \right)\) cắt nhau theo giao tuyến c thì hai đường thẳng a và c có song song với nhau hay không, hai đường thẳng b và c có song song với nhau hay không?
Hãy rút ra kết luận sau khi trả lời các câu hỏi trên.
Lời giải chi tiết:
Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng \(\left( \beta \right)\) thì \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau.
Video hướng dẫn giải
Trong không gian, cho bốn điểm A, B, C, D không đồng phẳng. Qua điểm A vẽ hai đường thẳng m; n lần lượt song song với hai đường thẳng BC, BD. Chứng minh rằng mp(m, n) song song với mặt phẳng (BCD)
Phương pháp giải:
Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng \(\left( \beta \right)\) thì \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau.
Lời giải chi tiết:

Ta có: m // BC suy ra m // (BCD).
n // BD suy ra n // (BCD).
Mặt phẳng (m,n) chứa hai đường thẳng cắt nhau m và n cùng song song với mặt phẳng (BCD) nên mặt phẳng (m, n) song song với mặt phẳng (BCD).
Video hướng dẫn giải
Một chiếc bàn có phần chân là hai khung sắt hình chữ nhật có thể xoay quanh một trục như trong Hình 4.43. Khi mặt bàn được đặt lên phần chân bàn thì mặt bàn luôn song song với mặt đất. Hãy giải thích tại sao.

Phương pháp giải:
Hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau nếu chúng không có điểm chung.
Lời giải chi tiết:
Do mặt bàn và mặt đất không có điểm chung nên chúng song song với nhau.
Video hướng dẫn giải
Đặt một tấm bìa cứng lên một góc của mặt bàn nằm ngang (H.4.44) sao cho mặt bìa song song với mặt đất. Khi đó mặt bìa có trùng với mặt bàn hay không?

Phương pháp giải:
Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.
Lời giải chi tiết:
Mặt bìa trùng với mặt bàn.
Video hướng dẫn giải
Cho hình chóp S.ABCD. Gọi M, N, P, Q lần lượt là các điểm thuộc các cạnh SA, SB, SC, SD sao cho
\(\frac{{MA}}{{MS}} = \frac{{NB}}{{NS}} = \frac{{PC}}{{PS}} = \frac{{QD}}{{QS}} = \frac{1}{2}\). Chứng minh rẳng bốn điểm M, N, P, Q đồng phẳng.
Phương pháp giải:
Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng \(\left( \beta \right)\) thì \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau.
Lời giải chi tiết:

Xét tam giác SAD có: \(\frac{{MA}}{{MS}} = \frac{{QD}}{{QS}}\) suy ra MQ // AD do đó MQ // (ABCD)
Tương tự ta có: QP // (ABCD)
Vậy mp(MPQ) // mp(ABCD).
Lập luận tương tự, ta có mp(NPQ) // (ABCD).
Hai mặt phẳng (MPQ) và (NPQ) cùng đi qua điểm P và cùng song song với mặt phẳng (ABCD) nên hai mặt phẳng đó trùng nhau, tức bốn điểm M, N, P, Q đồng phẳng.
Video hướng dẫn giải
Cho hai mặt phẳng song song (P) và (Q). Giả sử mặt phẳng (R) cắt mặt phẳng (P) theo giao tuyến a (H.4.46)
a) Giải thích vì sao mặt phẳng (R) cắt mặt phẳng (Q).
b) Gọi b là giao tuyến của hai mặt phẳng (R) và (Q). Hai đường thẳng a và b có thể chéo nhau hay không, có thể cắt nhau hay không?

Phương pháp giải:
Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
Lời giải chi tiết:
a) Vì (P) // (Q), (R) cắt (P) suy ra (R) cũng cắt (Q).
b) a và b lần lượt là giao tuyến của (R) và các mp(P), (Q) do đó a và b đồng phẳng suy ra a và b không thể chéo nhau.
Mà a và b lần lượt thuộc hai mặt phẳng song song (P) và (Q) suy ra a // b.
Video hướng dẫn giải
Trong Ví dụ 3, hãy xác định giao tuyến của mặt phẳng (EMQ) và mặt phẳng (ABCD).
Phương pháp giải:
Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
Lời giải chi tiết:

Ta có (MNPQ) // (ABCD) (chứng minh ở Ví dụ 2)
Vì vậy giao tuyến của (EMQ) với hai mặt phẳng (MNPQ) và (ABCD) song song với nhau
Trong mặt phẳng (EMQ), qua E vẽ đường thẳng ET // MQ (T thuộc CD)
Như vậy, đường thẳng ET là giao tuyến của (EMQ) và (ABCD).
Mục 2 của chương trình Toán 11 tập 1 - Kết nối tri thức tập trung vào các kiến thức về hàm số bậc hai. Các bài tập trang 89, 90, 91 SGK yêu cầu học sinh vận dụng các kiến thức đã học để xác định các yếu tố của hàm số bậc hai (hệ số a, b, c), tìm tập xác định, tập giá trị, đỉnh của parabol, vẽ đồ thị hàm số và giải các bài toán liên quan đến ứng dụng của hàm số bậc hai.
Bài tập này yêu cầu học sinh xác định các hệ số a, b, c của hàm số bậc hai được cho dưới dạng tổng quát y = ax2 + bx + c. Để làm được bài này, học sinh cần nắm vững định nghĩa của hàm số bậc hai và biết cách nhận biết các hệ số a, b, c.
Tập xác định của hàm số bậc hai là tập hợp tất cả các giá trị của x mà tại đó hàm số có nghĩa. Tập giá trị của hàm số là tập hợp tất cả các giá trị của y mà hàm số có thể nhận được. Để tìm tập xác định và tập giá trị của hàm số, học sinh cần xét dấu của hệ số a và tọa độ đỉnh của parabol.
Đỉnh của parabol là điểm thấp nhất (nếu a > 0) hoặc điểm cao nhất (nếu a < 0) của đồ thị hàm số bậc hai. Tọa độ đỉnh của parabol được tính theo công thức:
Để vẽ đồ thị hàm số bậc hai, học sinh cần thực hiện các bước sau:
Các bài toán ứng dụng hàm số bậc hai thường liên quan đến việc tìm giá trị lớn nhất, giá trị nhỏ nhất của một đại lượng nào đó, hoặc tìm điều kiện để một bài toán có nghiệm. Để giải các bài toán này, học sinh cần hiểu rõ ý nghĩa của hàm số bậc hai và biết cách thiết lập phương trình bậc hai để giải quyết bài toán.
Để giải tốt các bài tập về hàm số bậc hai, học sinh cần:
Ngoài sách giáo khoa, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng với những hướng dẫn chi tiết trên, các em học sinh sẽ tự tin giải quyết các bài tập trong mục 2 trang 89, 90, 91 SGK Toán 11 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!