Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 1 - Kết nối tri thức. Mục 4 trang 66 là một phần quan trọng trong chương trình học, đòi hỏi học sinh nắm vững kiến thức và kỹ năng giải quyết vấn đề.
Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, từng bước, giúp bạn hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
Với số liệu cho trong Luyện tập 1: a) Có thể tìm được giá trị chính xác cho mốt của mẫu số liệu gốc về thời gian xem ti vi của học sinh không? b) Mốt thuộc nhóm nào là hợp lí nhất? Nên lấy số nào trong nhóm để ước lượng cho mốt? Cho mẫu số liệu ghép nhóm như trong Bảng 3.2.
Video hướng dẫn giải
Với số liệu cho trong Luyện tập 1:
a) Có thể tìm được giá trị chính xác cho mốt của mẫu số liệu gốc về thời gian xem ti vi của học sinh không?
b) Mốt thuộc nhóm nào là hợp lí nhất? Nên lấy số nào trong nhóm để ước lượng cho mốt? Cho mẫu số liệu ghép nhóm như trong Bảng 3.2.
Phương pháp giải:
Mốt của mẫu số liệu ghép nhóm xấp xỉ cho mốt của mẫu số liệu gốc, nó được dùng để đo xu thể trung tâm của mẫu số liệu.
Lời giải chi tiết:
a) Không thể tìm được giá trị chính xác cho mốt của mẫu số liệu gốc về thời gian xem ti vi của học sinh
b) Tần số lớn nhất là 16 nên nhóm chứa mốt là [5;10)
Ta có \(j = 2,\;{a_2} = 5,\;{m_2} = 16,\;{m_1} = 8;\;{m_3} = 4,\;h = 5.\) Do đó,
\({M_0} = 5 + \frac{{16 - 8}}{{\left( {16 - 8} \right) + \left( {16 - 4} \right)}} \times 5 = 7\).
Video hướng dẫn giải
Thời gian (phút) để học sinh hoàn thành một câu hỏi thi được cho như sau:

Tìm mốt của mẫu số liệu ghép nhóm này.
Phương pháp giải:
Để tìm mốt của mẫu số liệu ghép nhóm, ta thực hiện theo các bước sau:
Bước 1: Xác định nhóm có tần số lớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm \(j:\left[ {{a_j};\;{a_{j + 1}}} \right)\)
Bước 2: Mốt được xác định là: \({M_0} = {a_j} + \frac{{{m_j} - {m_{j - 1}}}}{{\left( {{m_j} - {m_{j - 1}}} \right) + \left( {{m_j} - {m_{j + 1}}} \right)}}.h\)
Trong đó \({m_j}\) là tần số của nhóm j (quy ước \({m_0} = {m_{k + 1}} = 0)\) và h là độ dài của nhóm.
Lời giải chi tiết:
Tần số lớn nhất là 10 nên nhóm chứa mốt là [10.5;20.5]
Ta có \(j = 2,\;{a_2} = 10.5,\;{m_2} = 10,\;{m_1} = 2;\;{m_3} = 6,\;h = 10.\) Do đó,
\({M_0} = 10.5 + \frac{{10 - 2}}{{\left( {10 - 2} \right) + \left( {10 - 6} \right)}} \times 10 = 17.16\).
Video hướng dẫn giải
Hãy tính các số đặc trưng cho mẫu số liệu trong Bảng 3.1 và giải thích ý nghĩa của các giá trị thu được.

Phương pháp giải:
Sử dụng công thức số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\bar x\)
\(\bar x = \frac{{{m_1}{x_1} + \ldots + {m_k}{x_k}}}{n}\)
Trong đó \(n = {m_1} + \ldots + {m_k}\) là cỡ mẫu và là giá trị đại diện của nhóm \(\left[ {{a_i},{a_{i + 1}}} \right)\)
Để tính trung vị của mẫu số liệu ghép nhóm, ta làm như sau:
Bước 1: Xác định nhóm chưa trung vị. Giả sử đó là nhóm thứ \(p:\left[ {{a_p};\;{a_{p + 1}}} \right)\).
Bước 2: Trung vị là \({M_e} = {a_p} + \frac{{\frac{n}{2} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}}.\;\left( {{a_{p - 1}} - {a_p}} \right),\)
Trong đó n là cỡ mẫu, \({m_p}\)là tần số nhóm p. Với \(p = 1\), ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\)
Để tìm mốt của mẫu số liệu ghép nhóm, ta thực hiện theo các bước sau:
Bước 1: Xác định nhóm có tần sốớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm \(j:\left[ {{a_j};\;{a_{j + 1}}} \right)\).
Bước 2: Mốt được xác định là: \({M_0} = {a_j} + \frac{{{m_j} - {m_{j - 1}}}}{{\left( {{m_j} - {m_{j - 1}}} \right) + \left( {{m_j} - {m_{j + 1}}} \right)}}.h\).
Trong đó \({m_j}\) là tần số của nhóm j (quy ước \({m_0} = {m_{k + 1}} = 0)\) và h là độ dài của nhóm.
Lời giải chi tiết:
Ta có:
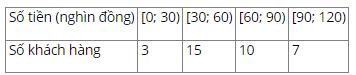
Số trung bình là \(\bar x = \frac{{3 \times 15 + 15 \times 45 + 10 \times 75 + 7 \times 105}}{{3 + 15 + 10 + 7}} = 63\)
Cỡ mẫu là: \(n = \;3\; + \;15\; + \;10\; + \;7\; = 35\)
Ý nghĩa: Xấp xỉ bằng số trung bình của mẫu số liệu gốc, cho biết vị trí trung tâm của mẫu số liệu và đại diện cho mẫu số liệu
Trung vị là \({x_{18}}\) thuộc nhóm \(\left[ {30;60} \right)\), do đó
\(p = 2,\;{a_2} = 30;\;{m_2} = 15;\;\;{m_1} = 3;\;\;{a_3} - {a_2} = 30\)và ta có:
\({M_e} = 30 + \frac{{\frac{{35}}{2} - 3}}{{15}} \times 30 = 59\).
Mục 4 trang 66 SGK Toán 11 tập 1 - Kết nối tri thức thường tập trung vào các bài toán liên quan đến phép biến hình, đặc biệt là phép tịnh tiến, phép quay, và phép đối xứng. Việc nắm vững các tính chất của các phép biến hình này là nền tảng để giải quyết các bài toán hình học phức tạp hơn trong chương trình học.
Mục 4 thường bao gồm các dạng bài tập sau:
Để giải quyết hiệu quả các bài toán trong Mục 4 trang 66, học sinh cần nắm vững các phương pháp sau:
Bài tập: Cho điểm A(1; 2) và phép tịnh tiến theo vectơ v = (3; -1). Tìm ảnh A' của điểm A qua phép tịnh tiến đó.
Lời giải:
Công thức phép tịnh tiến: A'(x' ; y') = A(x; y) + v(a; b) = (x + a; y + b)
Áp dụng công thức vào bài toán:
A'(x' ; y') = A(1; 2) + v(3; -1) = (1 + 3; 2 - 1) = (4; 1)
Vậy, ảnh A' của điểm A qua phép tịnh tiến theo vectơ v là A'(4; 1).
Để củng cố kiến thức và kỹ năng giải bài tập trong Mục 4 trang 66, học sinh nên:
Ngoài các kiến thức trong SGK, học sinh có thể tìm hiểu thêm về:
Hy vọng với những hướng dẫn chi tiết và phương pháp giải hiệu quả này, bạn sẽ tự tin chinh phục các bài tập trong Mục 4 trang 66 SGK Toán 11 tập 1 - Kết nối tri thức. Chúc bạn học tập tốt!