Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 3 trang 91 SGK Toán 11 tập 1 - Kết nối tri thức. Bài viết này cung cấp đáp án đầy đủ, chính xác, cùng với phương pháp giải rõ ràng, giúp học sinh dễ dàng nắm vững kiến thức và hoàn thành bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 11, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
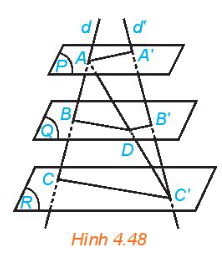
Cho mặt phẳng (P), (Q) và (R) đôi một song song. Hai đường thẳng phân biệt d và d’ cắt ba mặt phẳng lần lượt tại A, B, C và A’, B’, C’ (C khác C’). Gọi D là giao điểm của AC’ và (Q) (H.4.48) a) Các cặp đường thẳng BD và CC’, B’D và AA’ có song song với nhau không? b) Các tỉ số (frac{{AB}}{{BC}},frac{{AD}}{{DC'}}) và (frac{{A'B'}}{{B'C'}}) có bằng nhau không?
Video hướng dẫn giải
Cho mặt phẳng (P), (Q) và (R) đôi một song song. Hai đường thẳng phân biệt d và d’ cắt ba mặt phẳng lần lượt tại A, B, C và A’, B’, C’ (C khác C’). Gọi D là giao điểm của AC’ và (Q) (H.4.48)
a) Các cặp đường thẳng BD và CC’, B’D và AA’ có song song với nhau không?
b) Các tỉ số \(\frac{{AB}}{{BC}},\frac{{AD}}{{DC'}}\) và \(\frac{{A'B'}}{{B'C'}}\) có bằng nhau không?
Phương pháp giải:
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:
a) Mặt phẳng (Q) và (R) song song với nhau, suy ra giao tuyến của (ACC') với hai mặt phẳng (Q) và (R) song song với nhau. Do đó BD // CC'
Mặt phẳng (Q) và (P) song song với nhau, suy ra giao tuyến của (C'AA') với hai mặt phẳng (Q) và (P) song song với nhau. Do đó B'D // AA'
b) Xét tam giác ACC' ta có BD // CC' suy ra \(\frac{{AD}}{{BC}} = \frac{{AD}}{{DC'}}\)
Xét tam giác C'AA' ta có B'D // AA' suy ra \(ADDC' = A'B'B'C'\)
Do đó, \(\frac{{AB}}{{BC'}} = \frac{{AD}}{{DC'}} = \frac{{A'B'}}{{B'C'}}\)
Video hướng dẫn giải
Trong HĐ5, cho AB = 2cm, BC = 4cm và A’B’ =3cm. Tính độ dài của đoạn thẳng B’C’.
Phương pháp giải:
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết:
Áp dụng định lí Thales cho ba mặt phẳng đôi một song song (P), (Q), (R) và hai cát tuyến d, d' ta có:
\(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}}\) suy ra \(\frac{2}{4} = \frac{3}{{B'C'}}\)
=> B'C' = 6 (cm).
Mục 3 trang 91 SGK Toán 11 tập 1 - Kết nối tri thức thuộc chương trình học về hàm số lượng giác. Đây là một phần quan trọng trong chương trình Toán 11, đòi hỏi học sinh phải nắm vững các kiến thức cơ bản về hàm số, đồ thị hàm số và các phép biến đổi hàm số. Việc giải bài tập trong mục này giúp học sinh củng cố kiến thức, rèn luyện kỹ năng và chuẩn bị cho các bài kiểm tra, thi cử.
Mục 3 tập trung vào việc xét tính đơn điệu của hàm số lượng giác. Cụ thể, học sinh sẽ được hướng dẫn cách:
Mục 3 trang 91 SGK Toán 11 tập 1 - Kết nối tri thức bao gồm các bài tập khác nhau, từ các bài tập cơ bản đến các bài tập nâng cao. Các bài tập này yêu cầu học sinh phải:
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong mục 3 trang 91:
Để xét tính đơn điệu của hàm số y = sin(x) trên khoảng (0, π), ta tính đạo hàm của hàm số:
y' = cos(x)
Trên khoảng (0, π), cos(x) > 0. Do đó, hàm số y = sin(x) đồng biến trên khoảng (0, π).
Hàm số y = 2cos(x) - 1 có giá trị lớn nhất khi cos(x) đạt giá trị lớn nhất, tức là cos(x) = 1. Khi đó:
y = 2(1) - 1 = 1
Vậy, giá trị lớn nhất của hàm số y = 2cos(x) - 1 là 1.
Khi giải các bài tập về hàm số lượng giác, học sinh cần lưu ý những điều sau:
Để học tốt môn Toán 11, học sinh có thể tham khảo các tài liệu sau:
Việc giải bài tập mục 3 trang 91 SGK Toán 11 tập 1 - Kết nối tri thức là một bước quan trọng trong quá trình học tập môn Toán 11. Hy vọng rằng, với hướng dẫn chi tiết và các lưu ý trên, học sinh sẽ tự tin hơn khi giải các bài tập về hàm số lượng giác và đạt kết quả tốt trong học tập.