Bài 4.3 trang 77 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho mặt phẳng (P) và hai đường thẳng a, b nằm trong (P). Một đường thẳng c cắt hai đường thẳng a và b taij hai điểm phân biệt. Chứng minh rằng đường thẳng c nằm trong giao tuyến của hai mặt phẳng (ABM) và (SCD).
Đề bài
Cho mặt phẳng (P) và hai đường thẳng a, b nằm trong (P). Một đường thẳng c cắt hai đường thẳng a và b taij hai điểm phân biệt. Chứng minh rằng đường thẳng c nằm trong giao tuyến của hai mặt phẳng (ABM) và (SCD).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Để chứng minh giao tuyến của hai mặt phẳng, ta tìm hai điểm cùng thuộc cả hai mặt phẳng đó.
Lời giải chi tiết
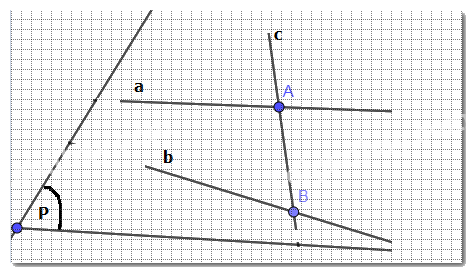
Đường thẳng c cắt hai đường thẳng a, b lần lượt tại A và B
Ta có A thuộc a mà a nằm trong mp(P) suy ra A cũng nằm trong mp(P)
B thuộc b mà b nằm trong mp(P) suy ra B cũng nằm trong mp(P)
Suy ra đường thẳng AB cũng nằm trong mp(P) tức c cũng nằm trong mp(P).
Bài 4.3 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc ứng dụng đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi của hàm số. Bài tập này thường xuất hiện trong các đề thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng cần thiết.
Bài 4.3 thường yêu cầu học sinh tính đạo hàm của một hàm số tại một điểm cụ thể, hoặc tìm đạo hàm của hàm số trong một khoảng xác định. Ngoài ra, bài tập có thể yêu cầu học sinh sử dụng đạo hàm để giải các bài toán về tối ưu hóa, chẳng hạn như tìm giá trị lớn nhất hoặc nhỏ nhất của một hàm số.
Để giải bài 4.3 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức, học sinh cần nắm vững các kiến thức sau:
Giả sử bài tập yêu cầu tính đạo hàm của hàm số f(x) = x2 + 2x - 1 tại điểm x = 1.
Ngoài việc tính đạo hàm tại một điểm, bài 4.3 còn có thể xuất hiện các dạng bài tập sau:
Để nắm vững kiến thức về đạo hàm và rèn luyện kỹ năng giải bài tập, học sinh nên thực hành giải nhiều bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập đa dạng, phong phú, giúp học sinh củng cố kiến thức và tự tin hơn trong các kỳ thi.
Ngoài SGK Toán 11 tập 1 - Kết nối tri thức, học sinh có thể tham khảo thêm các tài liệu sau:
Để học tốt môn Toán 11, học sinh cần:
Hy vọng với những hướng dẫn chi tiết và bài giải mẫu trên, các em học sinh sẽ tự tin hơn khi giải bài 4.3 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức. Chúc các em học tốt!