Chào mừng bạn đến với bài học lý thuyết Hàm số mũ và hàm số lôgarit dành cho học sinh lớp 11 chương trình Kết nối tri thức. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng quan trọng về hai loại hàm số đặc biệt này.
Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất, đồ thị và các ứng dụng thực tế của hàm số mũ và hàm số lôgarit.
1. Hàm số mũ a) Khái niệm hàm số mũ
1. Hàm số mũ
a) Khái niệm hàm số mũ
Cho a là số thực dương khác 1.
Hàm số \(y = {a^x}\) được gọi là hàm số mũ cơ số a.
b) Đồ thị và tính chất của hàm số mũ
Hàm số mũ \(y = {a^x}\):
- Có tập xác định là \(\mathbb{R}\) và tập giá trị là \(\left( {0; + \infty } \right)\);
- Đồng biến trên \(\mathbb{R}\) khi a > 1 và nghịch biến trên \(\mathbb{R}\) khi 0 < a < 1;
- Liên tục trên \(\mathbb{R}\);
- Có đồ thị đi qua các điểm (0; 1), (1; a) và luôn nằm phía trên trục hoành.
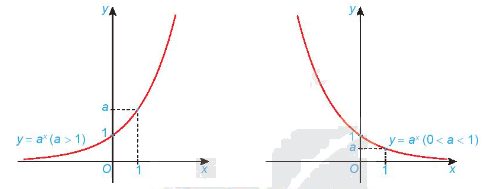
Dạng đồ thị của hàm số \(y = {a^x}\)
2. Hàm số lôgarit
a) Khái niệm hàm số lôgarit
Cho a là số thực dương khác 1.
Hàm số \(y = {\log _a}x\) được gọi là hàm số lôgarit cơ số a.
b) Đồ thị và tính chất của hàm số lôgarit
Hàm số lôgarit \(y = {\log _a}x\):
- Có tập xác định là \(\left( {0; + \infty } \right)\) và tập giá trị là \(\mathbb{R}\);
- Đồng biến trên \(\left( {0; + \infty } \right)\) khi a > 1 và nghịch biến trên \(\left( {0; + \infty } \right)\) khi 0 < a < 1;
- Có đồ thị đi qua các điểm (1; 0), (a; 1) và luôn nằm bên phải trục tung.
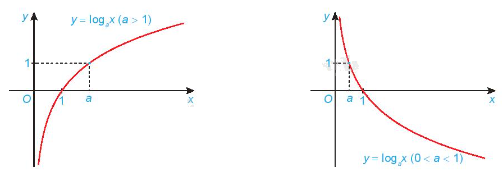
Dạng đồ thị của hàm số \(y = {\log _a}x\)
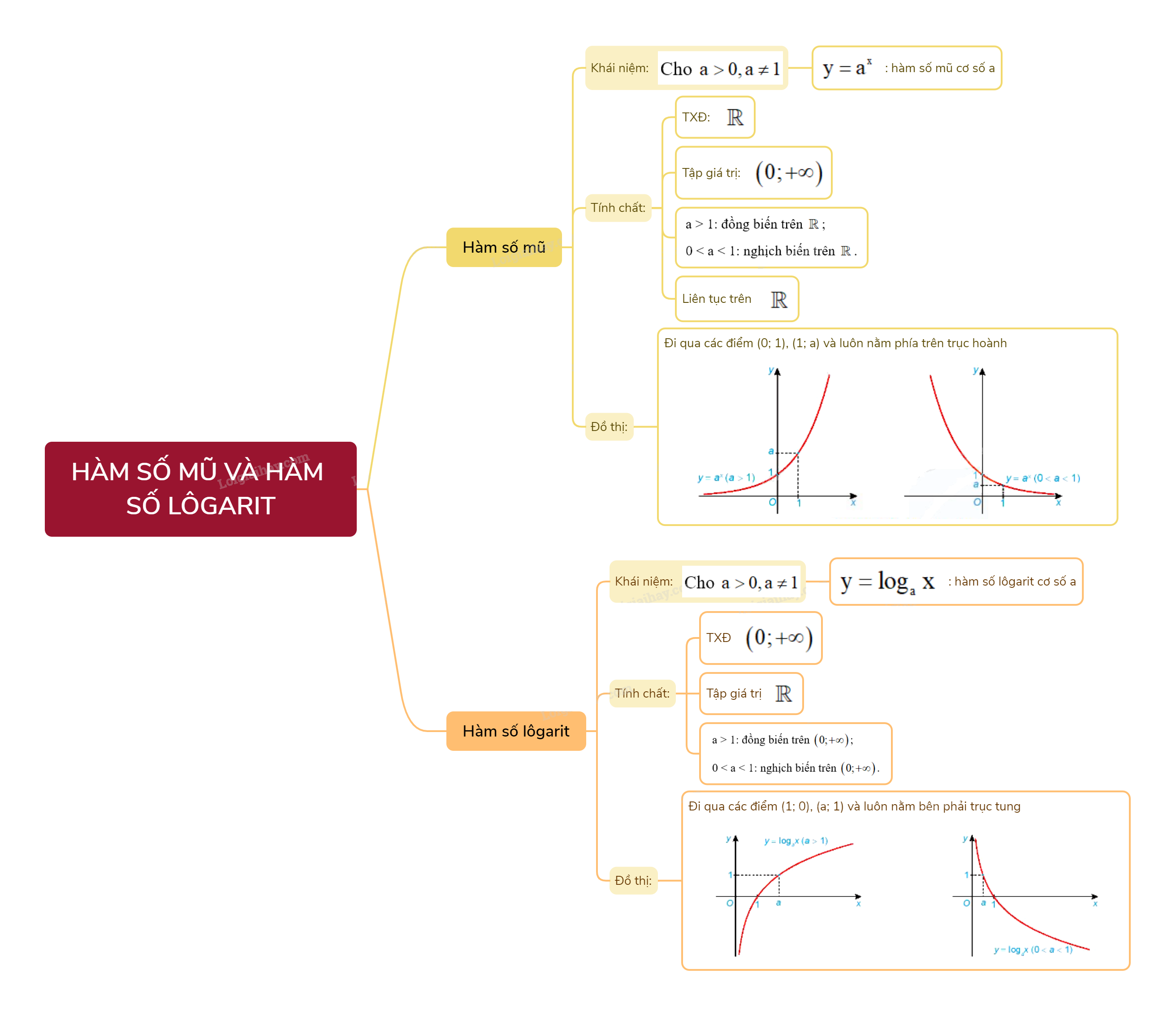
Hàm số mũ và hàm số lôgarit là hai khái niệm quan trọng trong chương trình Toán 11, chương trình Kết nối tri thức. Việc nắm vững lý thuyết và kỹ năng giải bài tập liên quan đến hai hàm số này là điều cần thiết để đạt kết quả tốt trong các kỳ thi và ứng dụng vào thực tế.
1. Định nghĩa: Hàm số mũ là hàm số có dạng y = ax, trong đó a là một số thực dương khác 1 (a > 0 và a ≠ 1). x là biến số.
2. Tập xác định: Tập xác định của hàm số mũ y = ax là tập số thực ℝ.
3. Tính chất:
1. Định nghĩa: Hàm số lôgarit là hàm số có dạng y = logax, trong đó a là một số thực dương khác 1 (a > 0 và a ≠ 1). x là biến số.
2. Tập xác định: Tập xác định của hàm số lôgarit y = logax là tập hợp các số thực dương (x > 0).
3. Tính chất:
Hàm số mũ và hàm số lôgarit là hai hàm số nghịch đảo của nhau. Điều này có nghĩa là:
1. Xác định tập xác định của hàm số: Yêu cầu học sinh xác định điều kiện để hàm số có nghĩa.
2. Tìm giá trị của hàm số: Thay giá trị của x vào hàm số để tính giá trị tương ứng của y.
3. Giải phương trình mũ và phương trình lôgarit: Sử dụng các tính chất của hàm số mũ và hàm số lôgarit để giải phương trình.
4. Khảo sát hàm số: Xác định tập xác định, tập giá trị, tính đơn điệu, cực trị và vẽ đồ thị hàm số.
Hàm số mũ và hàm số lôgarit có nhiều ứng dụng trong các lĩnh vực khác nhau của đời sống và khoa học, như:
Hy vọng bài học này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết Hàm số mũ và hàm số lôgarit - Toán 11 Kết nối tri thức. Chúc bạn học tập tốt!