Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 120, 121 sách giáo khoa Toán 11 tập 1 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho hai hàm số (fleft( x right) = left{ {begin{array}{*{20}{c}}{2x;,;0 le x le frac{1}{2}}{1;,frac{1}{2} < x le 1}end{array}} right.) và (gleft( x right) = left{ {begin{array}{*{20}{c}}{x;,0 le x le frac{1}{2}}{1;,frac{1}{2} < x le 1}end{array}} right.)
Video hướng dẫn giải
Cho hai hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{2x\;,\;0 \le x \le \frac{1}{2}}\\{1\;,\frac{1}{2} < x \le 1}\end{array}} \right.\) và \(g\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x\;,0 \le x \le \frac{1}{2}}\\{1\;,\frac{1}{2} < x \le 1}\end{array}} \right.\)với đồ thị tương ứng như Hình 5.7
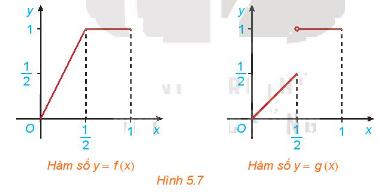
Xét tính liên tục của các hàm số f(x) và g(x) tại điểm \(x = \frac{1}{2}\)và nhận xét về sự khác nhau giữa hai đồ thị.
Phương pháp giải:
Hàm số \(f\left( x \right)\) liên tục trên khoảng \(\left( {a,b} \right)\) nếu nó liên tục tại mọi điểm thuộc khoảng này
Hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a,b} \right]\) nếu nó liên tục trên khoảng \(\left( {a,b} \right)\) và
\(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = f\left( a \right),\;\) \(\mathop {\lim }\limits_{x \to {b^ - }} f\left( x \right) = f\left( b \right)\)
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ - }} 2x = 1\)
\(\mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ + }} 1 = 1\)
\(f\left( {\frac{1}{2}} \right) = 1\)
Vậy \(f\left( x \right)\) liên tục tại \(x = \frac{1}{2}\)
\(\mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ - }} g\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ - }} x = \frac{1}{2}\)
\(\mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ - }} 1 = 1\)
\(g\left( {\frac{1}{2}} \right) = \frac{1}{2}\)
Vậy \(g\left( x \right)\) gián đoạn tại \(x = \frac{1}{2}\)
Đồ thị \(f\left( x \right)\) liên tục trên đoạn \(\left[ {0;1} \right],\) đồ thị \(g\left( x \right)\) bị gián đoạn tại \(x = \frac{1}{2}\)
Video hướng dẫn giải
Tìm các khoảng trên đó hàm số \(f\left( x \right) = \frac{{{x^2} + 1}}{{x + 2}}\) liên tục.
Phương pháp giải:
Hàm phân thức liên tục trên tập xác định.
Lời giải chi tiết:
Tập xác định của \(f\left( x \right)\) là \(\left( { - \infty ;\; - 2} \right) \cup \left( { - 2;\; + \infty } \right)\)
Vây hàm số \(f\left( x \right)\) liên tục trên các khoảng \(\left( { - \infty ; - 2} \right);\left( { - 2; + \infty } \right)\).
Mục 2 của chương trình Toán 11 tập 1 Kết nối tri thức tập trung vào các kiến thức về phép biến hình. Cụ thể, các em sẽ được làm quen với các phép biến hình cơ bản như phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các phép biến hình này là nền tảng quan trọng để học tập các kiến thức tiếp theo trong chương trình hình học.
Trang 120 và 121 SGK Toán 11 tập 1 Kết nối tri thức bao gồm các bài tập vận dụng kiến thức về phép biến hình để giải quyết các bài toán thực tế. Các bài tập này thường yêu cầu các em xác định ảnh của một điểm, một đường thẳng hoặc một hình qua một phép biến hình cho trước. Ngoài ra, các em cũng cần chứng minh một số tính chất liên quan đến phép biến hình.
Bài 1 yêu cầu các em thực hiện phép tịnh tiến một điểm hoặc một hình. Để giải bài này, các em cần hiểu rõ định nghĩa của phép tịnh tiến và cách xác định ảnh của một điểm qua phép tịnh tiến. Công thức tổng quát của phép tịnh tiến là:
x' = x + a
y' = y + b
Trong đó, (x, y) là tọa độ của điểm ban đầu và (x', y') là tọa độ của điểm ảnh sau phép tịnh tiến với vectơ tịnh tiến (a, b).
Bài 2 yêu cầu các em thực hiện phép quay một điểm hoặc một hình. Để giải bài này, các em cần hiểu rõ định nghĩa của phép quay và cách xác định ảnh của một điểm qua phép quay. Công thức tổng quát của phép quay quanh gốc tọa độ O một góc α là:
x' = x cos α - y sin α
y' = x sin α + y cos α
Bài 3 yêu cầu các em thực hiện phép đối xứng trục một điểm hoặc một hình. Để giải bài này, các em cần hiểu rõ định nghĩa của phép đối xứng trục và cách xác định ảnh của một điểm qua phép đối xứng trục. Ảnh của một điểm M(x, y) qua trục Ox là điểm M'(x, -y). Ảnh của một điểm M(x, y) qua trục Oy là điểm M'(-x, y).
Bài 4 yêu cầu các em thực hiện phép đối xứng tâm một điểm hoặc một hình. Để giải bài này, các em cần hiểu rõ định nghĩa của phép đối xứng tâm và cách xác định ảnh của một điểm qua phép đối xứng tâm. Ảnh của một điểm M(x, y) qua điểm I(a, b) là điểm M'(2a - x, 2b - y).
Phép biến hình có rất nhiều ứng dụng trong thực tế, chẳng hạn như trong thiết kế đồ họa, xây dựng, hàng không vũ trụ và nhiều lĩnh vực khác. Ví dụ, trong thiết kế đồ họa, phép biến hình được sử dụng để tạo ra các hiệu ứng đặc biệt, thay đổi kích thước và hình dạng của các đối tượng. Trong xây dựng, phép biến hình được sử dụng để tạo ra các bản vẽ kỹ thuật và mô hình 3D.
Hy vọng rằng với lời giải chi tiết và dễ hiểu này, các em sẽ nắm vững kiến thức về phép biến hình và giải quyết thành công các bài tập trong mục 2 trang 120, 121 SGK Toán 11 tập 1 Kết nối tri thức. Chúc các em học tập tốt!