Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3, trang 115, 116, 117 và 118 của sách giáo khoa Toán 11 tập 1 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt trong môn Toán.
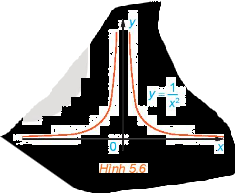
Xét hàm số (fleft( x right) = frac{1}{{{x^2}}}) có đồ thị như Hình 5.6. Cho ({x_n} = frac{1}{n}), chứng tỏ rằng (fleft( {{x_n}} right) to + infty )
Video hướng dẫn giải
Xét hàm số \(f\left( x \right) = \frac{1}{{{x^2}}}\) có đồ thị như Hình 5.6. Cho \({x_n} = \frac{1}{n}\), chứng tỏ rằng \(f\left( {{x_n}} \right) \to + \infty \)
Phương pháp giải:
Giả sử khoảng (a;b) chứa \({x_0}\) và hàm số \(y = f\left( x \right)\) xác định trên \(\left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}\). Ta nói hàm số \(f\left( x \right)\) có giới hạn \( + \infty \) khi \(x \to {x_0}\) nếu dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} \in \left( {a;b} \right)\backslash \left\{ {{x_0}} \right\},\;{x_n} \to {x_0}\), ta có \(f\left( {{x_n}} \right) \to + \infty ,\) kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = + \infty \)
Ta nói hàm số \(f\left( x \right)\) có giới hạn \( - \infty \) khi \(x \to \;{x_0}\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = - \infty \), nếu \(\mathop {\lim }\limits_{x \to {x_0}} \left[ { - f\left( x \right)} \right] = + \infty \)
Lời giải chi tiết:
Ta có: \(\mathbb{R}\backslash \left\{ 0 \right\}\)
\(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} f\left( {{x_n}} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{{{\left( {\frac{1}{n}} \right)}^2}}} = \mathop {\lim }\limits_{x \to + \infty } {n^2} = + \infty \).
Vậy \(f\left( {{x_n}} \right) \to + \infty \).
Video hướng dẫn giải
Cho hàm số \(f\left( x \right) = \frac{1}{{x - 1}}\). Với cá dãy số \(\left( {{x_n}} \right)\) và \(\left( {{{x'}_n}} \right)\) cho bởi \({x_n} = 1 + \frac{1}{n},\;x{'_n} = 1 - \frac{1}{n},\) tính \(\mathop {{\rm{lim}}}\limits_{n \to + \infty } f\left( {{x_n}} \right)\) và \(\mathop {{\rm{lim}}}\limits_{n \to + \infty } f\left( {x{'_n}} \right)\).
Phương pháp giải:
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \(\left( {{x_0};b} \right)\). Ta nói hàm số \(f\left( x \right)\) có giới hạn \( + \infty \) khi \(x \to {x_0}\) về bên phải nếu với dãy số \(\left( {{x_0}} \right)\) bất kì thỏa mãn \({x_0} < {x_n} < b,\;{x_n} \to {x_0}\), ta có \(f\left( {{x_n}} \right) \to + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = + \infty \).
Lời giải chi tiết:
\(\mathop {\lim }\limits_{x \to + \infty } f\left( {{x_n}} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{1 + \frac{1}{n} - 1}} = + \infty \).
\(\mathop {\lim }\limits_{x \to + \infty } f(x{'_n}) = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{1 - \frac{1}{n} - 1}} = - \infty \).
Video hướng dẫn giải
a) \(\mathop {{\rm{lim}}}\limits_{x \to 0 } \frac{2}{{\left| x \right|}}\) ;
b) \(\mathop {{\rm{lim}}}\limits_{x \to {2^ - }} \frac{1}{{\sqrt {2 - x} }}\)
Phương pháp giải:
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \(\left( {a;\;{x_0}} \right)\). Ta nói hàm số \(f\left( x \right)\) có giới hạn \( + \infty \) khi \(x \to {x_0}\) về bên trái nếu với dãy số \(\left( {{x_n}} \right)\) bất kì thỏa mãn \(a < {x_n} < {x_0},\;{x_n} \to {x_0}\), ta có \(f\left( {{x_n}} \right) \to + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = + \infty \).
Lời giải chi tiết:
a) \(\mathop {\lim }\limits_{x \to 0} \frac{2}{{\left| x \right|}} = + \infty \).
b)\(\mathop {\lim }\limits_{x \to {2^ - }} \frac{1}{{\sqrt {2 - x} }} = + \infty \;\).
Video hướng dẫn giải
Tính:\(\mathop {{\rm{lim}}}\limits_{x \to {2^ + }} \frac{{2x - 1}}{{x - 2}}\) và \(\mathop {{\rm{lim}}}\limits_{x \to {2^ - }} \frac{{2x - 1}}{{x - 2}}\).
Phương pháp giải:
Áp dụng quy tắc tìm giới hạn của thương.
Lời giải chi tiết:
\(x \to {2^ + } \Rightarrow x - 2 > 0\)
\(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{2x - 1}}{{x - 2}} = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{2 \times 2 - 1}}{{x - 2}} = + \infty \;\).
\(x \to {2^ - } \Rightarrow x - 2 < 0\)
\(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{2x - 2}}{{x - 2}} = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{2 \times 2 - 1}}{{x - 2}} = - \infty \).
Mục 3 của chương trình Toán 11 tập 1 - Kết nối tri thức tập trung vào các kiến thức về vectơ trong không gian. Các bài tập trong mục này yêu cầu học sinh vận dụng các định lý, tính chất của vectơ để giải quyết các bài toán liên quan đến vị trí tương đối của điểm và đường thẳng, chứng minh đẳng thức vectơ, và tính độ dài vectơ.
Bài 1 (trang 115): Bài tập này yêu cầu học sinh xác định tọa độ của vectơ, thực hiện các phép toán cộng, trừ, nhân với một số thực trên vectơ. Để giải bài tập này, học sinh cần nắm vững các quy tắc về tọa độ của vectơ và các phép toán trên vectơ.
Bài 2 (trang 116): Bài tập này tập trung vào việc chứng minh các đẳng thức vectơ. Học sinh cần sử dụng các tính chất của vectơ, các quy tắc biến đổi vectơ để chứng minh các đẳng thức được cho.
Bài 3 (trang 117): Bài tập này yêu cầu học sinh tìm tọa độ của điểm thỏa mãn một điều kiện nào đó liên quan đến vectơ. Học sinh cần sử dụng các công thức về tọa độ trung điểm, trọng tâm của tam giác, và các công thức liên quan đến vectơ chỉ phương, vectơ pháp tuyến của đường thẳng.
Bài 4 (trang 118): Bài tập này là một bài toán ứng dụng thực tế, yêu cầu học sinh sử dụng kiến thức về vectơ để giải quyết một bài toán hình học không gian. Học sinh cần phân tích bài toán, vẽ hình, và sử dụng các công thức, định lý liên quan đến vectơ để tìm ra lời giải.
Để giải tốt các bài tập về vectơ trong không gian, học sinh cần:
Ví dụ: Cho A(1; 2; 3), B(4; 5; 6). Tìm tọa độ của điểm M sao cho M là trung điểm của đoạn thẳng AB.
Giải:
Tọa độ của trung điểm M của đoạn thẳng AB được tính theo công thức:
M = ((xA + xB)/2; (yA + yB)/2; (zA + zB)/2)
Thay tọa độ của A và B vào công thức, ta được:
M = ((1 + 4)/2; (2 + 5)/2; (3 + 6)/2) = (2.5; 3.5; 4.5)
Vậy tọa độ của điểm M là (2.5; 3.5; 4.5).
Để học tốt môn Toán 11, các em cần dành thời gian ôn tập kiến thức, làm bài tập đầy đủ, và tìm kiếm sự giúp đỡ của giáo viên hoặc bạn bè khi gặp khó khăn. Chúc các em học tập tốt!