Bài 11 trang 106 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Kết nối tri thức, tập trung vào việc ôn tập chương 4: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số lượng giác, các phép biến đổi lượng giác và giải phương trình lượng giác để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 11 trang 106, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và (SA bot (ABC),SA = asqrt 2 ).
Đề bài
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và \(SA \bot (ABC),SA = a\sqrt 2 \). Khoảng cách từ \(A\) đến mặt phẳng \((SBC)\) bằng
A. \(\frac{{6a}}{{11}}\).
B. \(\frac{{a\sqrt {66} }}{{11}}\).
C. \(\frac{{a\sqrt 6 }}{{11}}\).
D. \(\frac{{a\sqrt {11} }}{{11}}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Khoảng cách từ một điểm M đến một mặt phẳng (P) là khoảng cách giữa M và hình chiếu H của M trên (P)
Lời giải chi tiết
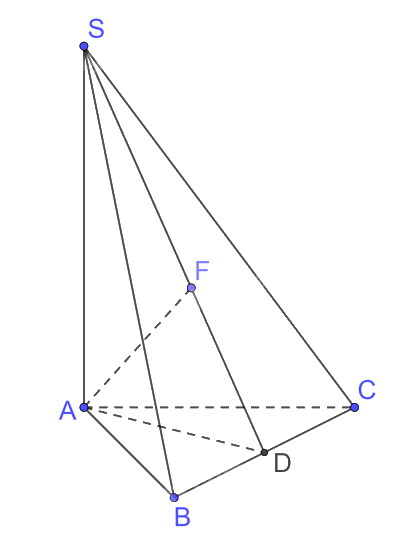
Trong (ABC) kẻ \(AD \bot BC\)
Mà tam giác ABC đều cạnh a nên \(AD = \frac{{a\sqrt 3 }}{2}\)
Ta có \(SA \bot BC,AD \bot BC \Rightarrow BC \bot \left( {SAD} \right);BC \subset \left( {SBC} \right) \Rightarrow \left( {SAD} \right) \bot \left( {SBC} \right)\)
Mà \(\left( {SAD} \right) \cap \left( {SBC} \right) = SD\)
Trong (SAD) kẻ \(AF \bot SD\)
Do đó \(AF \bot \left( {SBC} \right) \Rightarrow d\left( {A,\left( {SBC} \right)} \right) = AF\)
Xét tam giác SAD có
\(\frac{1}{{A{F^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{D^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = \frac{{11}}{{6{a^2}}} \Rightarrow AF = \frac{{\sqrt {66} }}{{11}}a\)
Vậy \(d\left( {A,\left( {SBC} \right)} \right) = \frac{{a\sqrt {66} }}{{11}}\)
Đáp án B
Bài 11 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức là một bài tập quan trọng trong chương trình ôn tập chương 4 về hàm số lượng giác. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
Dưới đây là lời giải chi tiết cho từng phần của Bài 11 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức:
Bài tập yêu cầu giải các phương trình lượng giác khác nhau. Để giải quyết, chúng ta cần áp dụng các công thức lượng giác và các phương pháp giải phương trình đã học. Ví dụ, để giải phương trình sin(x) = a, ta cần xác định các giá trị của x thỏa mãn điều kiện. Tương tự, đối với phương trình cos(x) = a hoặc tan(x) = a, chúng ta cũng cần áp dụng các công thức và phương pháp tương ứng.
Ví dụ: Giải phương trình sin(x) = 1/2.
Ta có sin(x) = 1/2 khi x = π/6 + k2π hoặc x = 5π/6 + k2π, với k là số nguyên.
Bài tập yêu cầu tìm giá trị lượng giác của một góc cho trước. Để làm điều này, chúng ta có thể sử dụng máy tính bỏ túi hoặc áp dụng các công thức lượng giác để tính toán. Ví dụ, để tìm sin(30°), ta có thể sử dụng máy tính hoặc nhớ rằng sin(30°) = 1/2.
Ví dụ: Tìm cos(45°).
Ta có cos(45°) = √2/2.
Bài tập yêu cầu chứng minh một đẳng thức lượng giác. Để chứng minh, chúng ta cần biến đổi một vế của đẳng thức để nó tương đương với vế còn lại. Việc này thường đòi hỏi sự khéo léo trong việc sử dụng các công thức lượng giác và các phép biến đổi đại số.
Ví dụ: Chứng minh sin2(x) + cos2(x) = 1.
Ta có thể chứng minh đẳng thức này bằng cách sử dụng định lý Pythagoras trong tam giác vuông.
Lưu ý khi giải bài tập:
Tầm quan trọng của việc học tốt hàm số lượng giác:
Hàm số lượng giác là một phần quan trọng của chương trình Toán học ở cấp THPT. Việc nắm vững kiến thức về hàm số lượng giác không chỉ giúp học sinh giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng cho việc học các môn học khác như Vật lý, Hóa học và các ngành kỹ thuật.
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh có thể tự tin giải quyết Bài 11 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức. Chúc các em học tốt!
| Hàm số | Định nghĩa |
|---|---|
| sin(x) | Tỉ số giữa cạnh đối và cạnh huyền trong tam giác vuông |
| cos(x) | Tỉ số giữa cạnh kề và cạnh huyền trong tam giác vuông |
| tan(x) | Tỉ số giữa cạnh đối và cạnh kề trong tam giác vuông |