Chào mừng bạn đến với chuyên mục lý thuyết công thức lượng giác của chương trình Toán 11 Kết nối tri thức tại giaitoan.edu.vn. Đây là phần kiến thức quan trọng, đặt nền móng cho các bài toán phức tạp hơn trong chương trình học.
Chúng tôi cung cấp hệ thống lý thuyết đầy đủ, chính xác, được trình bày một cách dễ hiểu, giúp bạn nắm bắt nhanh chóng và hiệu quả các khái niệm, định lý và công thức cần thiết.
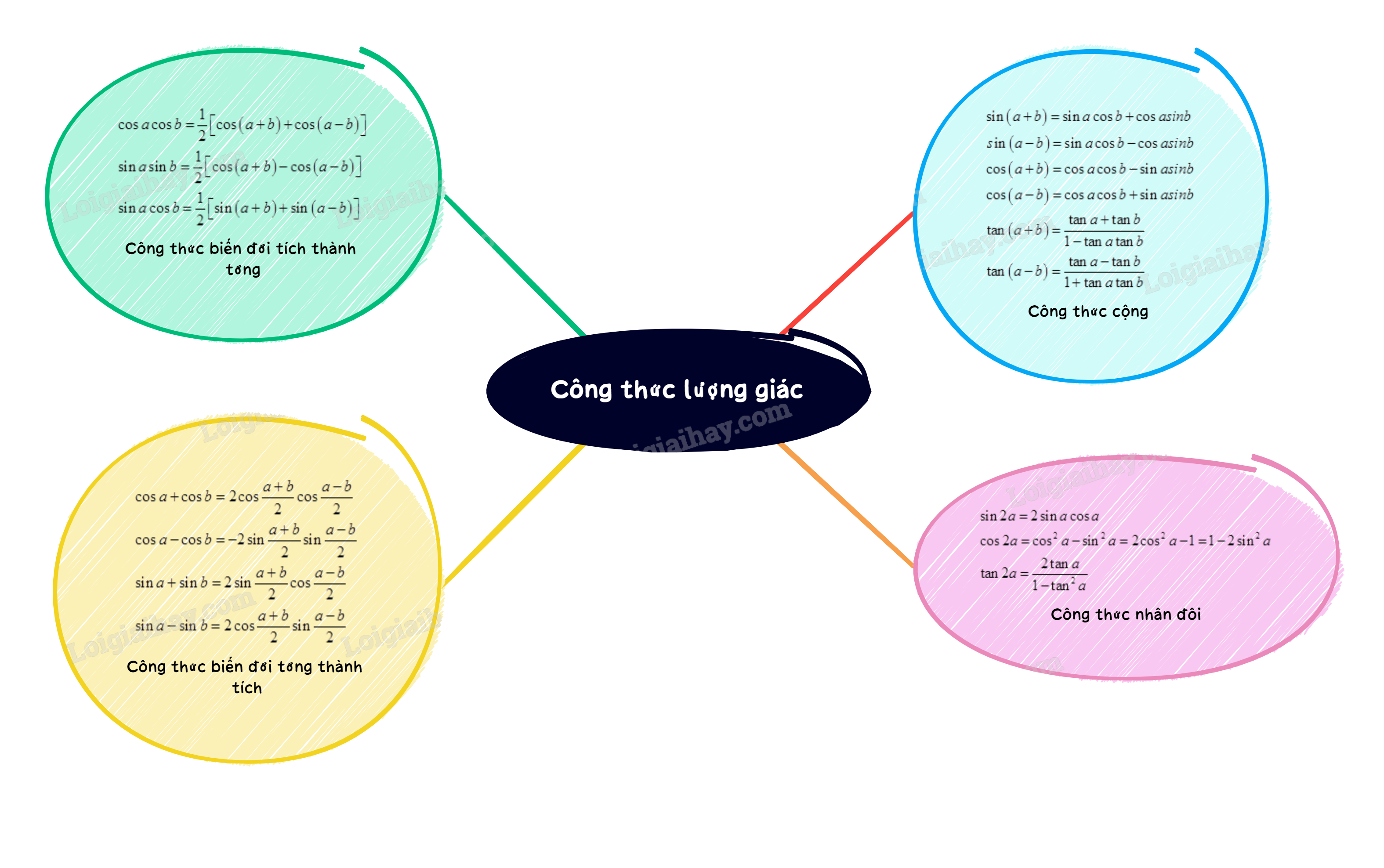
1. Công thức cộng
1. Công thức cộng
\(\begin{array}{l}\sin \left( {a + b} \right) = \sin a\cos b + \cos asinb\\sin\left( {a - b} \right) = \sin a\cos b - \cos asinb\\\cos \left( {a + b} \right) = \cos a\cos b - \sin asinb\\\cos \left( {a - b} \right) = \cos a\cos b + \sin asinb\\\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\\\tan \left( {a - b} \right) = \frac{{\tan a - \tan b}}{{1 + \tan a\tan b}}\end{array}\)
2. Công thức nhân đôi
\(\begin{array}{l}\sin 2a = 2\sin a\cos a\\\cos 2a = {\cos ^2}a - {\sin ^2}a = 2{\cos ^2}a - 1 = 1 - 2{\sin ^2}a\\\tan 2a = \frac{{2\tan a}}{{1 - {{\tan }^2}a}}\end{array}\)
Suy ra, công thức hạ bậc:
\({\sin ^2}a = \frac{{1 - \cos 2a}}{2},{\cos ^2}a = \frac{{1 + \cos 2a}}{2}\)
3. Công thức biến đổi tích thành tổng
\(\begin{array}{l}\cos a\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right]\\\sin a\sin b = \frac{1}{2}\left[ {\cos \left( {a - b} \right) - \cos \left( {a + b} \right)} \right]\\\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right]\end{array}\)
4. Công thức biến đổi tổng thành tích
\(\begin{array}{l}\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\\\cos a - \cos b = - 2\sin \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\\\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\\\sin a - \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\end{array}\)
Lượng giác là một nhánh quan trọng của toán học, nghiên cứu về mối quan hệ giữa các góc và cạnh của tam giác. Trong chương trình Toán 11 Kết nối tri thức, phần lượng giác đóng vai trò then chốt trong việc giải quyết các bài toán hình học và ứng dụng thực tế.
Góc lượng giác là góc được đo bằng độ hoặc radian. Để chuyển đổi giữa độ và radian, ta sử dụng công thức:
Các loại góc lượng giác thường gặp:
Các hàm số lượng giác cơ bản bao gồm:
Các giá trị lượng giác của một số góc đặc biệt:
| Góc (α) | sin(α) | cos(α) | tan(α) | cot(α) |
|---|---|---|---|---|
| 0° | 0 | 1 | 0 | Không xác định |
| 30° | 1/2 | √3/2 | 1/√3 | √3 |
| 45° | √2/2 | √2/2 | 1 | 1 |
| 60° | √3/2 | 1/2 | √3 | 1/√3 |
| 90° | 1 | 0 | Không xác định | 0 |
Các công thức lượng giác đóng vai trò quan trọng trong việc biến đổi và rút gọn các biểu thức lượng giác. Một số công thức cơ bản:
Các công thức cộng và hiệu lượng giác giúp tính toán giá trị lượng giác của tổng hoặc hiệu hai góc:
Các công thức nhân đôi và nhân ba lượng giác giúp tính toán giá trị lượng giác của góc gấp đôi hoặc gấp ba một góc:
Việc nắm vững các công thức lượng giác này là điều kiện cần thiết để giải quyết các bài toán lượng giác một cách hiệu quả. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của bạn.