Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 8, 9, 10 sách giáo khoa Toán 11 tập 1 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
a) Đổi từ độ sang rađian các số đo sau
Video hướng dẫn giải
a) Đổi từ độ sang rađian các số đo sau: \({360^ \circ }, - {450^ \circ }\)
b) Đổi từ rađian sang độ các số đo sau: \(3\pi , - \frac{{11\pi }}{5}\)
Phương pháp giải:
Áp dụng công thức:
\({\alpha ^ \circ } = \alpha .\frac{\pi }{{180}}rad\) ; \(\alpha \,rad = \alpha .{\left( {\frac{{180}}{\pi }} \right)^ \circ }\)
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}{360^ \circ } = 360.\frac{\pi }{{180}} = 2\pi \\ - {450^ \circ } = -450.\frac{\pi }{{180}} = -\frac{5}{2}\pi \end{array}\)
b)\(3\pi = 3\pi .{\left( {\frac{{180}}{\pi }} \right)^ \circ } = {540^ \circ }\)
\( - \frac{{11\pi }}{5} = \left( { - \frac{{11\pi }}{5}} \right).{\left( {\frac{{180}}{\pi }} \right)^ \circ } = - {396^ \circ }\)
Video hướng dẫn giải
Cho đường tròn bán kính R.
a) Độ dài của cung tròn có số đo bằng 1 rad là bao nhiêu
b) Tính độ dài l của cung tròn có số đo \(\alpha \)rad.
Phương pháp giải:
Áp dụng công thức tính độ dài cung tròn.
Lời giải chi tiết:
a) Độ dài của cung tròn có số đo bằng 1 rad là bằng bán kính R.
b) Độ dài l của cung tròn có số đo \(\alpha \) rad: \(l = R\alpha \).
Video hướng dẫn giải
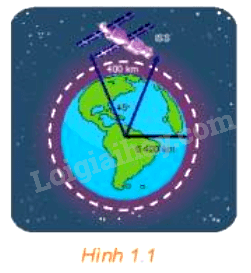
Trạm vũ trụ Quốc tế ISS (tên Tiếng Anh: International Space Station) nằm trong quỹ đạo tròn cách bề mặt Trái Đất khoảng 400 km (H.1.1). Nếu trạm mặt đất theo dõi được trạm vũ trụ ISS khi nó nằm trong góc 45° ở tâm của quỹ đạo tròn này phía trên ăng-ten theo dõi, thì trạm vũ trụ ISS đã di chuyển được bao nhiêu kilômét trong khi nó đang được trạm mặt đất theo dõi? Giả sử rằng bán kính của Trái Đất là 6 400 km. Làm tròn kết quả đến hàng đơn vị.
Phương pháp giải:
Một cung của đường tròn bán kính R và số đo \(\alpha \) rad thì có độ dài \(l = R\alpha \).
Lời giải chi tiết:
Bán kính quỹ đạo của trạm vũ trụ quốc tế là R = 6 400 + 400 = 6 800 (km).
Đổi \(45{}^\circ =45\cdot \frac{\pi }{180}=\frac{\pi }{4}\).
Vậy trong khi được trạm mặt đất theo dõi, trạm ISS đã di chuyển một quãng đường có độ dài là \(l = R\alpha \text{ = }6\,800\cdot \frac{\pi }{4}\approx 5\,340,708\approx 5\,341\,(km)\).
Mục 2 của SGK Toán 11 tập 1 Kết nối tri thức tập trung vào các kiến thức cơ bản về giới hạn của hàm số. Đây là một khái niệm quan trọng, nền tảng cho việc học tập các chương trình Toán học nâng cao hơn. Việc hiểu rõ về giới hạn hàm số giúp học sinh có thể giải quyết các bài toán liên quan đến đạo hàm, tích phân và các ứng dụng của Toán học trong thực tế.
Mục 2 bao gồm các nội dung chính sau:
Bài 1: Tính giới hạn của hàm số f(x) = 2x + 1 khi x tiến tới 2.
Lời giải:
lim (x→2) (2x + 1) = 2 * 2 + 1 = 5
Bài 2: Tính giới hạn của hàm số f(x) = x2 - 4 khi x tiến tới 2.
Lời giải:
lim (x→2) (x2 - 4) = 22 - 4 = 0
Bài 3: Tính giới hạn của hàm số f(x) = (x - 1) / (x + 1) khi x tiến tới 1.
Lời giải:
lim (x→1) (x - 1) / (x + 1) = (1 - 1) / (1 + 1) = 0 / 2 = 0
Bài 4: Tính giới hạn của hàm số f(x) = 1 / x khi x tiến tới 0+.
Lời giải:
lim (x→0+) 1 / x = +∞
Bài 5: Tính giới hạn của hàm số f(x) = sin(x) / x khi x tiến tới 0.
Lời giải:
lim (x→0) sin(x) / x = 1 (Đây là một giới hạn lượng giác cơ bản)
Bài 6: Tính giới hạn của hàm số f(x) = (ex - 1) / x khi x tiến tới 0.
Lời giải:
lim (x→0) (ex - 1) / x = 1 (Đây là một giới hạn đặc biệt liên quan đến hàm số mũ)
Giới hạn có nhiều ứng dụng trong thực tế, ví dụ:
Hy vọng rằng với lời giải chi tiết và các hướng dẫn trên, các em học sinh đã hiểu rõ hơn về cách giải các bài tập trong mục 2 trang 8,9,10 SGK Toán 11 tập 1 Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!