Bài 3.4 trang 67 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Kết nối tri thức. Bài học này tập trung vào việc giải quyết các bài toán liên quan đến vectơ, đặc biệt là các phép toán vectơ và ứng dụng của chúng trong hình học.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Quãng đường (km) từ nhà đến nơi làm việc của 40 công nhân một nhà máy được ghi lại như sau: 5 3 10 20 25 11 13 7 12 31 19 10 12 17 18 11 32 17 16 2 7 9 7 8 3 5 12 15 18 3 12 14 2 9 6 15 15 7 6 12
Đề bài
Quãng đường (km) từ nhà đến nơi làm việc của 40 công nhân một nhà máy được ghi lại như sau:
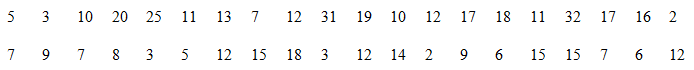
a) Ghép nhóm dãy số liệu trên thành các khoảng có độ rộng bằng nhau, khoảng đầu tiên là \(\left[ {0;5} \right)\). Tìm giá trị đại diện cho mỗi nhóm
b) Tính số trung bình của mẫu số liệu không ghép nhóm và mẫu số liệu ghép nhóm. Giá trị nào chính xác hơn?
c) Xác định nhóm chứa mốt của mẫu số liệu ghép nhóm thu được.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Giá trị đại diện của nhóm bằng trung bình giá trị đầu mút phải và trái của nhóm đó
Sử dụng công thức số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\bar x\)
\(\bar x = \frac{{{m_1}{x_1} + \ldots + {m_k}{x_k}}}{n}\)
Trong đó \(n = {m_1} + \ldots + {m_k}\) là cỡ mẫu và là giá trị đại diện của nhóm \(\left[ {{a_i},{a_{i + 1}}} \right)\)
Nhóm chứa mốt là nhóm có tần số lớn nhất.
Lời giải chi tiết
a)

b) Với mẫu số liệu không ghép nhóm:
\(\bar x = \left( {5 + 3 + 10 + 20 + 25 + 11 + 13 + 7 + 12 + 31 + 19 + 10 + 12 + 17 + 18 + 11 + 32 + 17 + 16 + 2 + 7 + 9 + 7 + 8 + 3 + 5 + 12 + 15 + 18 + 3 + 12 + 14 + 2 + 9 + 6 + 15 + 15 + 7 + 6 + 12} \right):40 = 11.9\)
Với mẫu số liệu ghép nhóm:
\(\bar x = \frac{{2.5 \times 5 + 7.5 \times 11 + 12.5 \times 11 + 17.5 \times 9 + 22.5 + 27.5 + 32.5 \times 2}}{{40}} = 12.625\).
Số trung bình của mẫu số liệu không ghép nhóm chính xác hơn.
c) 11 là tần số lớn nhất nên nhóm chứa mốt là \(\left[ {5;10} \right)\) hoặc \(\left[ {10;15} \right)\).
Bài 3.4 trang 67 SGK Toán 11 tập 1 - Kết nối tri thức là một phần quan trọng trong chương trình học Toán 11, tập trung vào việc củng cố kiến thức về vectơ và ứng dụng của chúng. Để giúp học sinh hiểu rõ hơn về bài học này, chúng ta sẽ cùng nhau đi sâu vào giải chi tiết từng phần của bài tập.
Bài 3.4 tập trung vào các nội dung sau:
Dưới đây là giải chi tiết các bài tập trong Bài 3.4 trang 67 SGK Toán 11 tập 1 - Kết nối tri thức:
Đề bài: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng: overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2
Lời giải:
Đề bài: Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh rằng: overrightarrow{OA} +overrightarrow{OC} =overrightarrow{0}
Lời giải:
Các kiến thức và kỹ năng được học trong Bài 3.4 có ứng dụng rộng rãi trong việc giải các bài toán hình học, đặc biệt là trong việc chứng minh các đẳng thức vectơ và giải các bài toán liên quan đến vị trí tương đối của các điểm và đường thẳng.
Để củng cố kiến thức, bạn có thể luyện tập thêm các bài tập tương tự trong sách bài tập Toán 11 tập 1 - Kết nối tri thức hoặc tìm kiếm trên các trang web học toán online.
Bài 3.4 trang 67 SGK Toán 11 tập 1 - Kết nối tri thức là một bài học quan trọng, giúp học sinh nắm vững kiến thức về vectơ và ứng dụng của chúng. Hy vọng rằng, với lời giải chi tiết và hướng dẫn trên, các bạn học sinh sẽ hiểu rõ hơn về bài học này và đạt kết quả tốt trong các kỳ thi.
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng. |
| Phép cộng vectơ | Quy tắc hình bình hành. |