Bài 4.25 trang 94 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Cho hình lăng trụ tứ giác ABCD. A’B’C’D’. Một mặt phẳng song song với mặt phẳng (A’B’C’D’) cắt các cạnh bên của hình lăng trụ lần lượt tại A”, B”, C”, D”. Hỏi hình tạo bởi các điểm A, B, C, D, A”, B”, C”, D” là hình gì?
Đề bài
Cho hình lăng trụ tứ giác ABCD. A’B’C’D’. Một mặt phẳng song song với mặt phẳng (A’B’C’D’) cắt các cạnh bên của hình lăng trụ lần lượt tại A”, B”, C”, D”. Hỏi hình tạo bởi các điểm A, B, C, D, A”, B”, C”, D” là hình gì?
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Hình lăng trụ có đáy là hình tam giác được gọi là hinh lăng trụ tam giác, hình lăng trụ có đáy là tứ giác được gọi là hình lăng trụ tứ giác.
Lời giải chi tiết
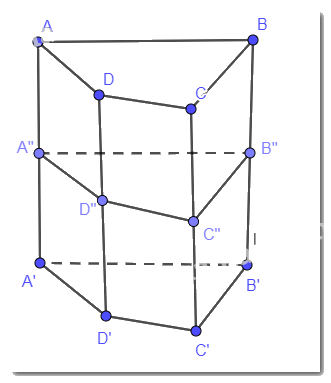
Vì các cạnh bên của hình lăng trụ ABCD.A'B'C'D' đôi một song song nên AA", BB", CC" đôi một song song.
Mặt phẳng (ABCD) song song với (A"B"C"D") (do cùng song song với (A'B'C'D')) nên ABCD.A"B"C"D" là hình lăng trụ tứ giác.
Bài 4.25 trang 94 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 11, tập trung vào việc ứng dụng đạo hàm để giải quyết các bài toán liên quan đến tốc độ thay đổi của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và công thức về đạo hàm, bao gồm đạo hàm của hàm số tại một điểm, đạo hàm của các hàm số cơ bản, và các quy tắc tính đạo hàm.
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu. Thông thường, bài tập này sẽ yêu cầu tính đạo hàm của một hàm số tại một điểm cụ thể, hoặc tìm điều kiện để hàm số có đạo hàm tại một điểm. Ngoài ra, đề bài có thể yêu cầu sử dụng đạo hàm để giải quyết các bài toán thực tế, chẳng hạn như tính vận tốc, gia tốc, hoặc tốc độ thay đổi của một đại lượng nào đó.
Giả sử đề bài yêu cầu tính đạo hàm của hàm số f(x) = x^2 + 2x + 1 tại điểm x = 1.
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Ngoài SGK Toán 11 tập 1 - Kết nối tri thức, học sinh có thể tham khảo thêm các tài liệu sau để học tập và luyện tập:
Giaitoan.edu.vn hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ tự tin hơn khi giải Bài 4.25 trang 94 SGK Toán 11 tập 1 - Kết nối tri thức và đạt kết quả tốt trong môn Toán.