Chào mừng bạn đến với chuyên mục Lý thuyết Dãy số của chương trình Toán 11 Kết nối tri thức tại giaitoan.edu.vn. Chúng tôi cung cấp đầy đủ và chi tiết các kiến thức quan trọng về dãy số, giúp bạn hiểu rõ bản chất và áp dụng hiệu quả vào giải bài tập.
Dãy số là một khái niệm nền tảng trong Toán học, đặc biệt quan trọng trong chương trình Toán 11. Việc nắm vững lý thuyết dãy số sẽ giúp bạn giải quyết các bài toán liên quan đến cấp số cộng, cấp số nhân, giới hạn dãy số và nhiều ứng dụng thực tế khác.
1. Định nghĩa dãy số
1. Định nghĩa dãy số
Mỗi hàm số u xác định trên tập các số nguyên dương \({\mathbb{N}^*}\) được gọi là một dãy số vô hạn (gọi tắt là dãy số). Kí hiệu là \(u = u\left( n \right)\).
Ta thường viết \({u_n}\) thay cho \(u\left( n \right)\) và kí hiệu dãy số \(u = u\left( n \right)\)bởi \(u\left( n \right)\), do đó dãy số \(\left( {{u_n}} \right)\)được viết dưới dạng khai triển \({u_1},{u_2},{u_3},...,{u_n},...\)
Số \({u_1}\) là số hạng đầu; \({u_n}\)là số hạng thứ n và gọi là số hạng tổng quát của dãy số.
*Chú ý: Nếu \(\forall n \in {\mathbb{N}^*},{u_n} = c\)thì \(\left( {{u_n}} \right)\)được gọi là dãy số không đổi.
Mỗi hàm số u xác định trên tập \(M = \left\{ {1;2;3;...;m} \right\},m \in {\mathbb{N}^*}\) được gọi là một dãy số hữu hạn.
Dạng khai triển của dãy số hữu hạn là \({u_1},{u_2},{u_3},...,{u_m}\).
Số \({u_1}\) gọi là số hạng đầu, \({u_m}\)là số hạng cuối.
2. Cách cho một dãy số
Một dãy số có thể cho bằng:
3. Dãy số tăng, dãy số giảm và dãy số bị chặn
Dãy số \(\left( {{u_n}} \right)\) được gọi là dãy số giảm nếu ta có \({u_{n + 1}} < {u_n}\)\(,\forall n \in {\mathbb{N}^*}\).
Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn dưới nếu \(\exists \) số m sao cho \({u_n} \ge m,\) \(\forall n \in {\mathbb{N}^*}\).
Dãy số \(\left( {{u_n}} \right)\) được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho \(m \le {u_n} \le M,\)\(\forall n \in {\mathbb{N}^*}\).
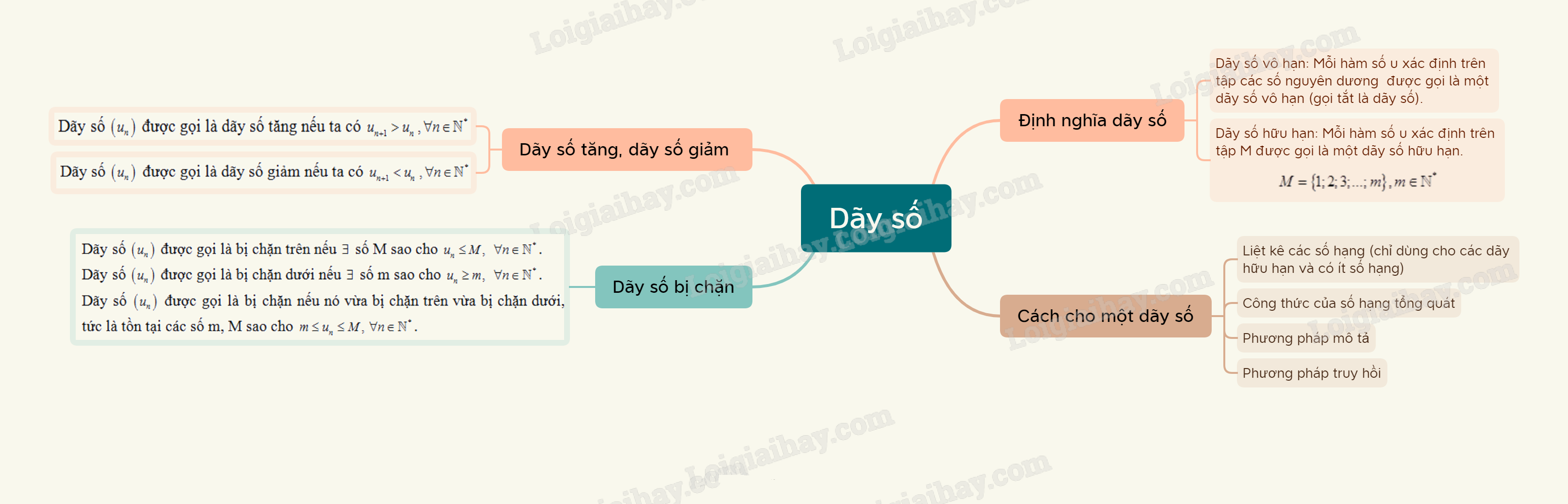
Dãy số là một tập hợp hữu hạn hoặc vô hạn các số thực được sắp xếp theo một thứ tự nhất định. Mỗi phần tử trong dãy số được gọi là một số hạng của dãy số. Dãy số thường được ký hiệu là (un), trong đó un là số hạng thứ n của dãy số.
Một dãy số (un) được gọi là dãy số nếu với mỗi số nguyên dương n, ta xác định được duy nhất một số thực un. Dãy số có thể hữu hạn (ví dụ: 1, 2, 3, 4, 5) hoặc vô hạn (ví dụ: 1, 2, 3, ...).
Công thức tổng quát của dãy số là một công thức cho phép tính số hạng thứ n của dãy số dựa trên giá trị của n. Ví dụ, dãy số (un) với un = 2n + 1 là một dãy số có công thức tổng quát.
Cấp số cộng là một dãy số mà mỗi số hạng sau đều lớn hơn (hoặc nhỏ hơn) số hạng trước một lượng không đổi, gọi là công sai (d). Công thức tổng quát của cấp số cộng là: un = u1 + (n - 1)d, trong đó u1 là số hạng đầu tiên.
Ví dụ: Dãy số 2, 5, 8, 11, ... là một cấp số cộng với u1 = 2 và d = 3.
Cấp số nhân là một dãy số mà mỗi số hạng sau đều bằng số hạng trước nhân với một lượng không đổi, gọi là công bội (q). Công thức tổng quát của cấp số nhân là: un = u1 * q(n-1), trong đó u1 là số hạng đầu tiên.
Ví dụ: Dãy số 3, 6, 12, 24, ... là một cấp số nhân với u1 = 3 và q = 2.
Giới hạn của dãy số là giá trị mà dãy số tiến tới khi n tiến tới vô cùng. Nếu dãy số (un) có giới hạn L, ta viết limn→∞ un = L.
Ví dụ: limn→∞ (1/n) = 0.
Lý thuyết dãy số có nhiều ứng dụng trong thực tế, bao gồm:
Để củng cố kiến thức về lý thuyết dãy số, bạn có thể thực hành giải các bài tập sau:
Hy vọng rằng những kiến thức về Lý thuyết Dãy số - SGK Toán 11 Kết nối tri thức này sẽ giúp bạn học tập tốt hơn. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải các bài toán thực tế.