Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 2 Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tối ưu nhất.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả cao trong học tập. Hãy cùng khám phá lời giải cho mục 1 trang 16, 17 SGK Toán 11 tập 2 ngay bây giờ!
a) Tính (y = {2^x}) khi x lần lượt nhận các giá trị - 1; 0; 1. Với mỗi giá trị của x có bao nhiêu giá trị của (y = {2^x}) tương ứng?
Video hướng dẫn giải
a) Tính \(y = {2^x}\) khi x lần lượt nhận các giá trị - 1; 0; 1. Với mỗi giá trị của x có bao nhiêu giá trị của \(y = {2^x}\) tương ứng?
b) Với những giá trị nào của x, biểu thức \(y = {2^x}\) có nghĩa?
Phương pháp giải:
Thay các giá trị x lần lượt để tính y.
Lời giải chi tiết:
a) Với \(x = - 1\) thì \(y = {2^{ - 1}} = \frac{1}{2}\)
Với \(x = 0\) thì \(y = {2^0} = 1\)
Với \(x = 1\) thì \(y = {2^1} = 2\)
b) Biểu thức \(y = {2^x}\) có nghĩa với mọi giá trị của x.
Video hướng dẫn giải
Trong các hàm số sau, những hàm số nào là hàm số mũ? Khi đó hãy chỉ ra cơ cố.
a) \(y = {\left( {\sqrt 2 } \right)^x};\)
b) \(y = {2^{ - x}};\)
c) \(y = {8^{\frac{x}{3}}};\)
d) \(y = {x^{ - 2}}.\)
Phương pháp giải:
Sử dụng định nghĩa hàm số mũ.
Lời giải chi tiết:
a) \(y = {\left( {\sqrt 2 } \right)^x}\) là hàm số mũ có cơ số là \(\sqrt 2 .\)
b) \(y = {2^{ - x}} = {\left( {{2^{ - 1}}} \right)^x}\) là hàm số mũ có cơ số là \({2^{ - 1}} = \frac{1}{2}.\)
c) \(y = {8^{\frac{x}{3}}} = {\left( {{8^{\frac{1}{3}}}} \right)^x} = {\left( {\sqrt[3]{8}} \right)^x}\) là hàm số mũ có cơ số là \({8^{\frac{1}{3}}} = \sqrt[3]{8} = 2.\)
d) \(y = {x^{ - 2}}\) không là hàm số mũ.
Video hướng dẫn giải
Cho hàm số mũ \(y = {2^x}.\)
a) Hoàn thành bảng giá trị sau:

b) Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; 2x) với \(x \in \mathbb{R}\) và nối lại ta được đồ thị của hàm số
c) Từ đồ thị đã vẽ ở câu b, hãy kết luận về tập giá trị và tính chất biến thiên của hàm số
Phương pháp giải:
Vẽ đồ thị dựa vào các điểm đã lấy sau đó nhìn đồ thị để đưa ra tập giá trị và tính chất biến thiên.
Lời giải chi tiết:
a)

b,
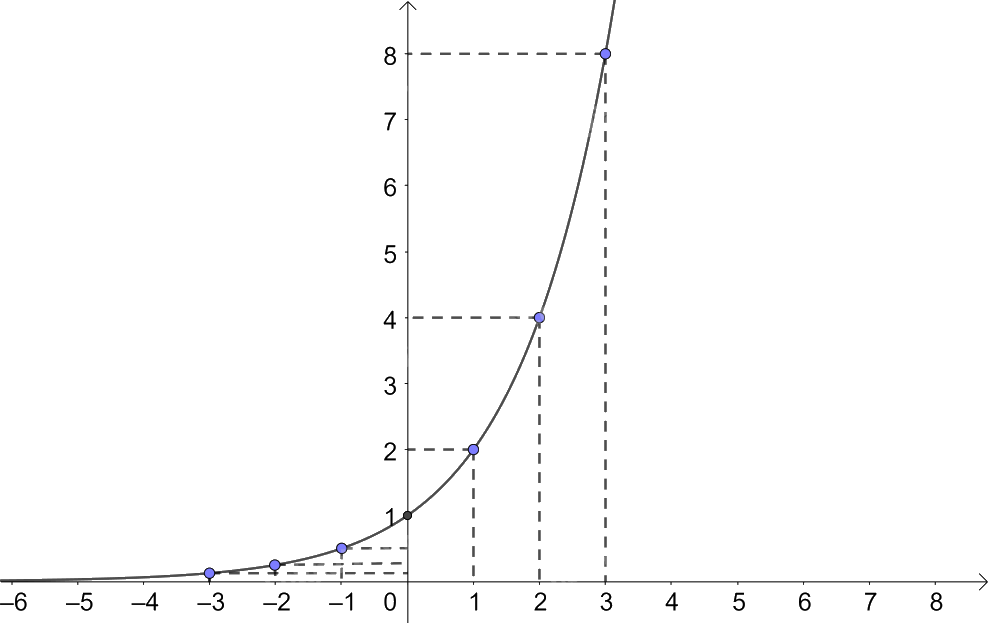
c) Tập giá trị: \(\left( {0; + \infty } \right)\)
Tính chất biến thiên: đồng biến
Video hướng dẫn giải
Vẽ đồ thị của hàm số \(y = {\left( {\frac{3}{2}} \right)^x}.\)
Phương pháp giải:
Lập bảng giá trị để vẽ đồ thị hàm số.
Lời giải chi tiết:
Lập bảng giá trị của hàm số tại một điểm như sau:

Từ đó, ta vẽ được đồ thị của hàm số:

Mục 1 của chương trình Toán 11 tập 2 Kết nối tri thức tập trung vào các kiến thức về phép biến hình. Cụ thể, học sinh sẽ được làm quen với các phép biến hình cơ bản như phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các phép biến hình này là nền tảng quan trọng để hiểu sâu hơn về hình học không gian và các ứng dụng của nó trong thực tế.
Bài tập mục 1 trang 16, 17 SGK Toán 11 tập 2 Kết nối tri thức bao gồm các dạng bài tập khác nhau, yêu cầu học sinh vận dụng kiến thức về các phép biến hình để giải quyết các vấn đề cụ thể. Các bài tập này thường xoay quanh việc xác định ảnh của một điểm, một đường thẳng hoặc một hình qua một phép biến hình nhất định. Ngoài ra, học sinh cũng cần phải chứng minh các tính chất liên quan đến các phép biến hình.
Để giúp học sinh hiểu rõ hơn về cách giải các bài tập trong mục 1 trang 16, 17, chúng tôi xin trình bày hướng dẫn giải chi tiết cho từng bài tập:
Bài tập này yêu cầu học sinh xác định ảnh của một điểm M qua phép tịnh tiến theo vectơ v. Để giải bài tập này, học sinh cần áp dụng công thức: M' = M + v, trong đó M' là ảnh của M qua phép tịnh tiến theo vectơ v.
Bài tập này yêu cầu học sinh xác định ảnh của một điểm M qua phép quay tâm O góc α. Để giải bài tập này, học sinh cần áp dụng công thức: M' = O + R(M - O), trong đó M' là ảnh của M qua phép quay tâm O góc α, R là ma trận quay.
Bài tập này yêu cầu học sinh xác định ảnh của một điểm M qua phép đối xứng trục d. Để giải bài tập này, học sinh cần tìm hình chiếu vuông góc của M lên d, sau đó xác định điểm M' sao cho d là đường trung trực của đoạn thẳng MM'.
Bài tập này yêu cầu học sinh xác định ảnh của một điểm M qua phép đối xứng tâm I. Để giải bài tập này, học sinh cần áp dụng công thức: M' = 2I - M, trong đó M' là ảnh của M qua phép đối xứng tâm I.
Các phép biến hình có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Hy vọng rằng với hướng dẫn giải chi tiết này, các bạn học sinh sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 16, 17 SGK Toán 11 tập 2 Kết nối tri thức. Chúc các bạn học tập tốt!
| Phép biến hình | Công thức |
|---|---|
| Tịnh tiến | M' = M + v |
| Quay | M' = O + R(M - O) |
| Đối xứng trục | Tìm hình chiếu vuông góc và sử dụng tính chất đường trung trực |
| Đối xứng tâm | M' = 2I - M |