Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 4, trang 13, 14, 15 và 16 của sách giáo khoa Toán 11 tập 1 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
a) Dựa vào định nghĩa của (sin alpha )và (cos alpha ) hãy tính ({sin ^2}alpha + {cos ^2}alpha ) b) Sử dụng kết quả của HĐ5a và định nghĩa của (tan alpha ), hãy tính (1 + {tan ^2}alpha )
Video hướng dẫn giải
a) Dựa vào định nghĩa của \(\sin \alpha \)và \(\cos \alpha \) hãy tính \({\sin ^2}\alpha + {\cos ^2}\alpha \)
b) Sử dụng kết quả của HĐ5a và định nghĩa của \(\tan \alpha \), hãy tính \(1 + {\tan ^2}\alpha \)
Phương pháp giải:
Vẽ hình. Xác định các điểm \(\sin \alpha \) và \(\cos \alpha \) trên hình.
Sử dụng định lý Pytago để tính
Lời giải chi tiết:
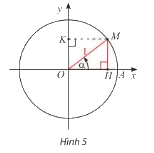
a) Trong Hình 5, M là điểm biểu diễn của góc lượng giác \(\alpha \) trên đường tròn lượng giác. Ta có:
OK = MH = \(\sin \alpha \)
OH = KM = \(\cos \alpha \)
\(\begin{array}{l}O{M^2} = O{H^2} + M{H^2}\\ \Rightarrow 1 = {\sin ^2}\alpha + {\cos ^2}\alpha \end{array}\)
b) \(1 + {\tan ^2}\alpha = \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\)
Video hướng dẫn giải
Tính các giá trị lượng giác của góc \(\alpha \), biết \(\cos \alpha = - \frac{2}{3}\) và \(\pi < \alpha < \frac{{3\pi }}{2}\)
Phương pháp giải:
Sử dụng hệ thức lượng giác cơ bản để tính giá trị lượng giác góc \(\alpha \). Chú ý dấu của giá trị lượng giác.
Lời giải chi tiết:
Vì \(\pi < \alpha < \frac{{3\pi }}{2}\)nên \(\sin \alpha < 0\). Mặc khác, từ \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) suy ra
\(\sin \alpha = -\sqrt {1 - {{\cos }^2}\alpha } = -\sqrt {1 - \frac{4}{9}} = -\frac{{\sqrt 5 }}{3}\)
Do đó \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{-\frac{{\sqrt 5 }}{3}}}{{ - \frac{2}{3}}} = \frac{{\sqrt 5 }}{2};\cot \alpha = \frac{1}{{\tan \alpha }} = \frac{{ 2}}{{\sqrt 5 }}\)
Video hướng dẫn giải
Xét hai điểm M, N trên đường tròn lượng giác xác định bởi hai góc đối nhau (H1.12a).
a) Có nhận xét gì về vị trí của hai điểm M, N đổi với hệ trục Oxy. Từ đó rút ra liên hệ giữa \(\cos ( - \alpha )\) và \(\cos \alpha \); \(\sin ( - \alpha )\)và \(\sin \alpha \)
b) Từ kết quả HĐ6a, rút ra liên hệ giữa: \(\tan ( - \alpha )\) và \(\tan \alpha \); \(\cot ( - \alpha )\) và \(\cot \alpha \)
Phương pháp giải:
Dựa vào hình vẽ để nhận xét
Lời giải chi tiết:

a) Hai điểm M và N đối xứng nhau qua hệ trục Oxy.
Suy ra
\(\cos ( - \alpha )\)=\(\cos \alpha \); \(\sin ( - \alpha )\)= \( - \sin \alpha \)
b) Ta có:
\(\tan ( - \alpha )\) =\( - \tan \alpha \); \(\cot ( - \alpha )\)\( - \cot \alpha \)
Video hướng dẫn giải
Tính: a) \(\sin ( - {675^ \circ })\) b) \(\tan \frac{{15\pi }}{4}\)
Phương pháp giải:
Áp dụng liên hệ giữa các giá trị lượng giác của các góc có liên quan đặc biệt.
Lời giải chi tiết:
Ta có: \(\sin ( - {675^ \circ }) = \sin ({45^ \circ } - {2.360^ \circ }) = \sin {45^ \circ } = \frac{{\sqrt 2 }}{2}\)
\(\tan \frac{{15\pi }}{4} = \tan \left( {3\pi + \frac{{3\pi }}{4}} \right) = \tan \left( {\pi + \frac{{3\pi }}{4}} \right) = \tan \left( {\frac{{3\pi }}{4}} \right) = \tan \left( {\pi - \frac{\pi }{4}} \right) = - \tan \left( {\frac{\pi }{4}} \right) = - 1\)
Video hướng dẫn giải
Huyết áp của mỗi người thay đổi trong ngày. Giả sử huyết áp trương (tức là áp lực máu lên thành động mạch khi tim giãn ra) của một người nào đó ở trạng thái nghỉ ngơi tại thời điểm t được cho bởi công thức:
\(B(t) = 80 + 7.\sin \frac{{\pi t}}{{12}}\)
Trong đó t là số giờ tính từ lúc nửa đêm và B(t) tính bằng mmHg (milimét thủy ngân). Tìm huyết áp tâm trương của người này vào cá thời điểm sau:
a) 6 giờ sáng b) 10 giờ 30 phút sáng; c) 12 giờ trưa d) 8 giờ tối
Phương pháp giải:
Tính thời gian t
Áp dụng liên hệ giữa các giá trị lượng giác giữa các góc có liên quan đặc biệt.
Lời giải chi tiết:
a) t = 6
\( \Rightarrow B(6) = 80 + 7.\sin \frac{{\pi 6}}{{12}} = 80 + 7.\sin \frac{\pi }{2} = 87\)
b) t=10,5
\( \Rightarrow B(10,5) = 80 + 7.\sin \frac{{\pi 10,5}}{{12}} = 80 + 7.\sin \frac{{7\pi }}{8} = 82,67878\)
c) t=12
\( \Rightarrow B(12) = 80 + 7.\sin \frac{{\pi 12}}{{12}} = 80 + 7.\sin \pi = 80\)
d) t = 20
\(\begin{array}{l} \Rightarrow B(20) = 80 + 7.\sin \frac{{\pi 20}}{{12}} = 80 + 7.\sin \frac{{5\pi }}{3} = 80 + 7.\sin \left( {\pi + \frac{{2\pi }}{3}} \right) = 80 - 7.\sin \left( {\frac{{2\pi }}{3}} \right) = 80 - 7.\sin \left( {\pi - \frac{\pi }{3}} \right)\\ = 80 - 7.\sin \left( {\frac{\pi }{3}} \right) = \frac{{160 - 7\sqrt 3 }}{2}\end{array}\)
Mục 4 của chương trình Toán 11 tập 1 - Kết nối tri thức tập trung vào các kiến thức về véc tơ trong không gian. Đây là một phần quan trọng, đặt nền móng cho các kiến thức hình học không gian phức tạp hơn ở các lớp trên. Nội dung chính bao gồm:
Trang 13 SGK Toán 11 tập 1 - Kết nối tri thức thường chứa các bài tập về khái niệm véc tơ trong không gian. Các bài tập này yêu cầu học sinh:
Ví dụ, bài tập 1 yêu cầu xác định các véc tơ trong hình vẽ. Để giải bài tập này, học sinh cần nắm vững định nghĩa của véc tơ và cách xác định các yếu tố của véc tơ.
Trang 14 SGK Toán 11 tập 1 - Kết nối tri thức tập trung vào các bài tập về phép cộng, phép trừ véc tơ trong không gian. Các bài tập này yêu cầu học sinh:
Ví dụ, bài tập 2 yêu cầu tìm véc tơ tổng của hai véc tơ cho trước. Để giải bài tập này, học sinh có thể sử dụng quy tắc hình bình hành hoặc quy tắc tọa độ.
Trang 15 và 16 SGK Toán 11 tập 1 - Kết nối tri thức thường chứa các bài tập về hệ tọa độ trong không gian và ứng dụng của véc tơ trong không gian. Các bài tập này yêu cầu học sinh:
Ví dụ, bài tập 3 yêu cầu tìm tọa độ của một điểm biết tọa độ của các điểm khác và véc tơ chỉ phương. Để giải bài tập này, học sinh cần nắm vững công thức liên hệ giữa tọa độ của các điểm và tọa độ của véc tơ.
Để giải tốt các bài tập về véc tơ trong không gian, học sinh cần:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và những lời khuyên trên, các em sẽ tự tin hơn khi giải các bài tập về véc tơ trong không gian. Chúc các em học tập tốt!
| Công thức | Mô tả |
|---|---|
| AB = B - A | Véc tơ AB được tính bằng hiệu tọa độ của điểm B và điểm A. |
| |AB| = √( (xB - xA)² + (yB - yA)² + (zB - zA)² ) | Độ dài của véc tơ AB. |