Bài 1.36 thuộc chương 1: Hàm số và đồ thị của SGK Toán 11 tập 1 - Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai, điều kiện xác định và tập giá trị của hàm số để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
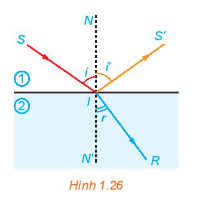
Khi một tia sáng truyền từ không khi vào mặt nước thì một phần tia sáng bị phản xạ trên bề mặt, phần còn lại bị khúc xạ như trong Hình 1.26.
Đề bài
Khi một tia sáng truyền từ không khi vào mặt nước thì một phần tia sáng bị phản xạ trên bề mặt, phần còn lại bị khúc xạ như trong Hình 1.26. Góc tới i liên hệ với góc khúc xạ r bởi Định luật khúc xạ ánh sáng
\(\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}}\)
Ở đây, \({n_1}\) và \({n_2}\) tương ứng là chiết suất của môi trường 1 (không khí) và môi trường 2 (nước). Cho biết góc tới \(i = {50^0}\), hãy tính góc khúc xạ, biết rằng chiết suất của không khí bằng 1 còn chiết suất của nước là 1,33.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Dùng công thức \(\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}}\) để tìm sin r. Từ đó, tìm số đo góc khúc xạ.
Lời giải chi tiết
Theo bài ra ta có: \(i = 50^\circ ,{\rm{ }}{n_1}\; = 1,{\rm{ }}{n_2}\; = 1,33\) thay vào \(\frac{{\sin i}}{{\sin r}} = \frac{{{n_2}}}{{{n_1}}}\) ta được:
\(\begin{array}{l}\frac{{\sin {{50}^o}}}{{\sin r}} = \frac{{1,33}}{1}\,(r \ne 0)\\ \Rightarrow \sin r = \frac{{\sin {{50}^o}}}{{1,33}} \approx 0,57597\,\,(TM)\\ \Leftrightarrow \left[ \begin{array}{l}r \approx {35^o}10' + k{360^o}\\r \approx {180^o} - {35^o}10' + k{360^o}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}r \approx {35^o}10' + k{360^o}\\r \approx {144^o}50' + k{360^o}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Mà \({0^o} < r < {90^o} \Rightarrow r \approx {35^o}10'\)
Vạy góc khúc xạ \(r \approx {35^o}10'\)
Bài 1.36 yêu cầu xét tính chẵn, lẻ của hàm số. Để giải bài này, học sinh cần nắm vững định nghĩa về hàm số chẵn, hàm số lẻ và cách kiểm tra chúng.
Để kiểm tra tính chẵn, lẻ của hàm số f(x) = 2x² - 1, ta xét f(-x):
f(-x) = 2(-x)² - 1 = 2x² - 1 = f(x)
Vì f(-x) = f(x) với mọi x thuộc tập xác định, nên hàm số f(x) = 2x² - 1 là hàm số chẵn.
Để kiểm tra tính chẵn, lẻ của hàm số g(x) = x³ + 2x, ta xét g(-x):
g(-x) = (-x)³ + 2(-x) = -x³ - 2x = -(x³ + 2x) = -g(x)
Vì g(-x) = -g(x) với mọi x thuộc tập xác định, nên hàm số g(x) = x³ + 2x là hàm số lẻ.
Để kiểm tra tính chẵn, lẻ của hàm số h(x) = x² + x + 1, ta xét h(-x):
h(-x) = (-x)² + (-x) + 1 = x² - x + 1
Ta thấy h(-x) ≠ h(x) và h(-x) ≠ -h(x) với mọi x thuộc tập xác định. Do đó, hàm số h(x) = x² + x + 1 không chẵn, không lẻ.
Để củng cố kiến thức về hàm số chẵn, lẻ, các em có thể tự giải các bài tập sau:
Bài 1.36 trang 41 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về khái niệm hàm số chẵn, hàm số lẻ và cách kiểm tra chúng. Việc nắm vững kiến thức này sẽ giúp các em giải quyết các bài toán liên quan một cách dễ dàng và hiệu quả.
| Hàm số | Tính chẵn, lẻ |
|---|---|
| f(x) = 2x² - 1 | Hàm số chẵn |
| g(x) = x³ + 2x | Hàm số lẻ |
| h(x) = x² + x + 1 | Không chẵn, không lẻ |