Bài 7.31 trang 63 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Kết nối tri thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế.
giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
khối lăng trụ ABC.A'B'C' có đáy là các tam giác đều cạnh a
Đề bài
Cho khối lăng trụ ABC.A'B'C' có đáy là các tam giác đều cạnh a, A'A = A'B = A'C = b. Tính thể tích của khối lăng trụ.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Thể tích khối lăng trụ \(V = h.S\)
Lời giải chi tiết
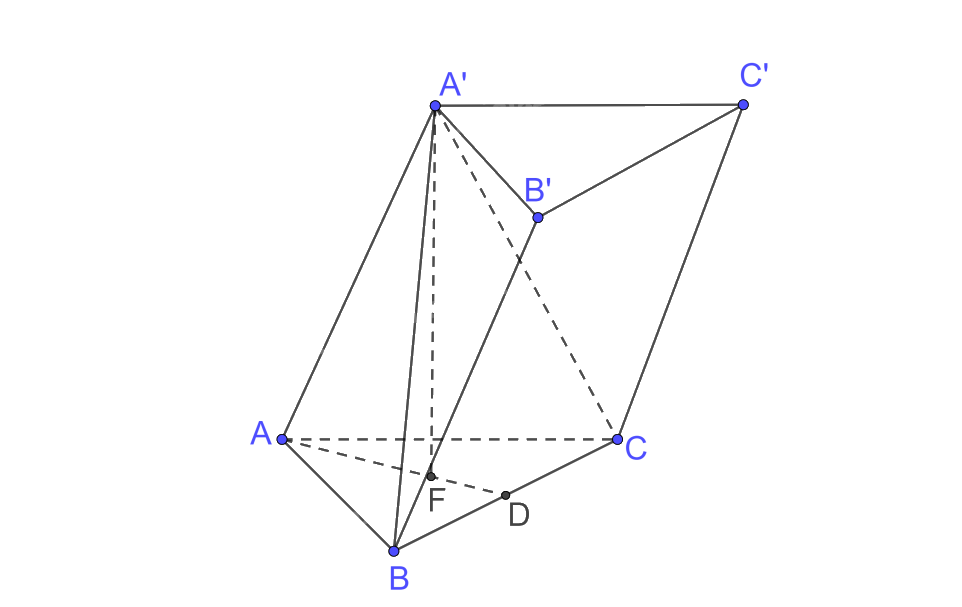
Vì hình chóp A’.ABC có A'A = A'B = A'C và đáy ABC là tam giác đều nên hình chóp A’.ABC đều.
Gọi F là hình chiếu của A’ trên (ABC) nên F là tâm của đáy ABC là tam giác đều do đó F cũng là trọng tâm của tam giác ABC.
Gọi AF cắt BC tại D
Tam giác ABC đều cạnh a nên \(AD = \frac{{a\sqrt 3 }}{2}\)
Mà F là trọng tâm nên \(AF = \frac{2}{3}AD = \frac{{a\sqrt 3 }}{3}\)
Xét tam giác A’AF vuông tại F có
\(A'F = \sqrt {A'{A^2} - A{F^2}} = \sqrt {{b^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} \)
Diện tích tam giác đều ABC là \(S = \frac{{{a^2}\sqrt 3 }}{4}\)
Thể tích khối lăng trụ là \(V = A'F.S = \sqrt {{b^2} - \frac{{{a^2}}}{3}} .\frac{{{a^2}\sqrt 3 }}{4}\)
Bài 7.31 trang 63 SGK Toán 11 tập 2 - Kết nối tri thức là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 7.31 yêu cầu học sinh xét hàm số f(x) = x3 - 3x2 + 2 và thực hiện các yêu cầu sau:
Tính đạo hàm f'(x).
Tìm các điểm cực trị của hàm số.
Xác định khoảng đồng biến và nghịch biến của hàm số.
Để tính đạo hàm f'(x), ta sử dụng quy tắc đạo hàm của hàm số đa thức:
f'(x) = 3x2 - 6x
Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2.
Để xác định xem các điểm này là điểm cực đại hay cực tiểu, ta xét dấu của đạo hàm bậc hai f''(x):
f''(x) = 6x - 6
Tại x = 0, f''(0) = -6 < 0, vậy x = 0 là điểm cực đại.
Tại x = 2, f''(2) = 6 > 0, vậy x = 2 là điểm cực tiểu.
Giá trị của hàm số tại các điểm cực trị là:
f(0) = 2
f(2) = 8 - 12 + 2 = -2
Vậy, hàm số có điểm cực đại là (0, 2) và điểm cực tiểu là (2, -2).
Ta xét dấu của đạo hàm f'(x):
f'(x) > 0 khi x < 0 hoặc x > 2, vậy hàm số đồng biến trên các khoảng (-∞, 0) và (2, +∞).
f'(x) < 0 khi 0 < x < 2, vậy hàm số nghịch biến trên khoảng (0, 2).
Thông qua việc giải bài 7.31 trang 63 SGK Toán 11 tập 2 - Kết nối tri thức, học sinh đã nắm vững kiến thức về đạo hàm, cách tìm điểm cực trị và xác định khoảng đồng biến, nghịch biến của hàm số. Đây là những kiến thức cơ bản và quan trọng trong chương trình học Toán 11.
Để hiểu rõ hơn về bài học, học sinh nên tự mình làm thêm các bài tập tương tự và tham khảo các tài liệu học tập khác. giaitoan.edu.vn luôn đồng hành cùng học sinh trên con đường chinh phục môn Toán.
Để giúp học sinh hiểu rõ hơn về cách giải bài tập, ta xét một ví dụ khác:
Cho hàm số g(x) = x4 - 4x2 + 3. Hãy tìm các điểm cực trị của hàm số.
Lời giải:
Tính đạo hàm g'(x) = 4x3 - 8x.
Giải phương trình g'(x) = 0: 4x3 - 8x = 0 => 4x(x2 - 2) = 0 => x = 0, x = √2, x = -√2.
Tính đạo hàm bậc hai g''(x) = 12x2 - 8.
Xác định dấu của g''(x) tại các điểm cực trị:
g''(0) = -8 < 0 => x = 0 là điểm cực đại.
g''(√2) = 16 > 0 => x = √2 là điểm cực tiểu.
g''(-√2) = 16 > 0 => x = -√2 là điểm cực tiểu.
Hy vọng với lời giải chi tiết và ví dụ minh họa trên, học sinh có thể tự tin giải quyết các bài tập tương tự trong SGK Toán 11 tập 2 - Kết nối tri thức.