Bài 1 trang 135 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải nắm vững các công thức đạo hàm cơ bản và kỹ năng giải toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 1 trang 135, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Anh Văn ghi lại cự li 30 lần ném lao của mình ở bảng sau (đơn vị: mét):
Đề bài
Anh Văn ghi lại cự li 30 lần ném lao của mình ở bảng sau (đơn vị: mét):

a) Tính cự li trung bình của mỗi lần ném.
b) Tổng hợp lại kết quả ném của anh Văn vào bảng tần số ghép nhóm theo mẫu sau:

c) Hãy ước lượng cự li trung bình mỗi lần ném từ bảng tần số ghép nhóm trên.
d) Khả năng anh Văn ném được khoảng bao nhiêu mét là cao nhất?
Phương pháp giải - Xem chi tiết
a) Sử dụng công thức tính trung bình cộng của mẫu số liệu.
b) Đếm và lập bảng.
c) Sử dụng công thức tính trung bình cộng của mẫu số liệu ghép nhóm.
d) Sử dụng công thức tính Mốt của mẫu số liệu ghép nhóm.
Lời giải chi tiết
a) Cự li trung bình của mỗi lần ném là: \(\bar x = 71,6\left( m \right)\).
b)

c)
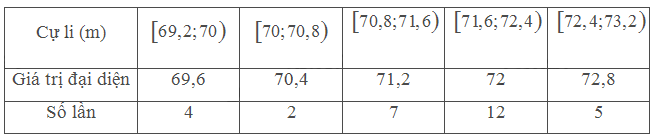
Cự li trung bình mỗi lần ném sau khi ghép nhóm là:
\(\bar x = \frac{{4.69,6 + 2.70,4 + 7.71,2 + 12.72 + 72,8.5}}{{30}} = 71,52\left( m \right)\)
d) Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\left[ {71,6;72,4} \right)\).
Do đó: \({u_m} = 71,6;{n_{m - 1}} = 7;{n_m} = 12;{n_{m + 1}} = 5;{u_{m + 1}} - {u_m} = 72,4 - 71,6 = 0,8\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 71,6 + \frac{{12 - 7}}{{\left( {12 - 7} \right) + \left( {12 - 5} \right)}}.0,8 \approx 71,9\left( m \right)\)
Vậy khả năng anh Văn ném được khoảng 71,9 mét là cao nhất.
Bài 1 trang 135 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 1 yêu cầu học sinh tính đạo hàm của các hàm số sau:
a) y = x3 - 3x2 + 2x - 5
b) y = (x2 + 1)(x - 2)
c) y = (x2 + 3x) / (x + 1)
d) y = sin(2x + 1)
Áp dụng công thức đạo hàm của tổng và hiệu, ta có:
y' = 3x2 - 6x + 2
Áp dụng quy tắc nhân, ta có:
y' = (2x)(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
Áp dụng quy tắc chia, ta có:
y' = [(2x + 3)(x + 1) - (x2 + 3x)(1)] / (x + 1)2 = (2x2 + 5x + 3 - x2 - 3x) / (x + 1)2 = (x2 + 2x + 3) / (x + 1)2
Áp dụng quy tắc hàm hợp, ta có:
y' = cos(2x + 1) * 2 = 2cos(2x + 1)
Để giải các bài tập tương tự, học sinh cần:
Nắm vững các công thức đạo hàm cơ bản của các hàm số đơn giản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit).
Hiểu rõ và áp dụng thành thạo các quy tắc đạo hàm (quy tắc tổng, hiệu, tích, thương, hàm hợp).
Luyện tập thường xuyên để rèn luyện kỹ năng giải toán.
Đạo hàm có rất nhiều ứng dụng trong toán học và các lĩnh vực khác, bao gồm:
Tìm cực trị của hàm số.
Khảo sát hàm số.
Tính tốc độ thay đổi của một đại lượng.
Giải các bài toán tối ưu hóa.
Khi giải bài tập về đạo hàm, học sinh cần chú ý:
Kiểm tra kỹ các công thức đạo hàm trước khi áp dụng.
Sử dụng đúng quy tắc đạo hàm.
Rút gọn biểu thức đạo hàm một cách cẩn thận.
Kiểm tra lại kết quả để đảm bảo tính chính xác.
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về Bài 1 trang 135 SGK Toán 11 tập 1 - Chân trời sáng tạo và tự tin giải các bài tập tương tự. Chúc các em học tốt!