Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 114, 115 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo. Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và lời giải dễ hiểu.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả tốt nhất trong môn Toán.
Cho mặt phẳng (left( P right)) chứa hai đường thẳng (a,b) cắt nhau và cùng song song với mặt phẳng (left( Q right)). Giả sử (left( P right)) và (left( Q right)) có điểm chung (M) thì (left( P right)) cắt (left( Q right)) theo giao tuyến (c) (Hình 5).
Cho mặt phẳng \(\left( P \right)\) chứa hai đường thẳng \(a,b\) cắt nhau và cùng song song với mặt phẳng \(\left( Q \right)\). Giả sử \(\left( P \right)\) và \(\left( Q \right)\) có điểm chung \(M\) thì \(\left( P \right)\) cắt \(\left( Q \right)\) theo giao tuyến \(c\) (Hình 5).
a) Giải thích tại sao đường thẳng \(c\) phải cắt ít nhất một trong hai đường thẳng \(a,b\). Điều này có trái với giả thiết \(a\) và \(b\) cùng song song với \(\left( Q \right)\) không?
b) Rút ra kết luận về số điểm chung và vị trí tương đối của \(\left( P \right)\) và \(\left( Q \right)\).
Phương pháp giải:
Sử dụng định lí:
‒ Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\). Nếu mặt phẳng \(\left( Q \right)\) chứa \(a\), cắt \(\left( P \right)\) theo giao tuyến \(b\) thì \(a\) song song với \(b\).
‒ Trong không gian, qua một điểm nằm ngoài một đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đó.
‒ Đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\) nếu chúng không có điểm chung.
Lời giải chi tiết:
a) Gọi \(I\) là giao điểm của \(a\) và \(b\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}a\parallel \left( Q \right)\\\left( P \right) \supset a\\\left( P \right) \cap \left( Q \right) = c\end{array} \right\} \Rightarrow c\parallel a\\\left. \begin{array}{l}b\parallel \left( Q \right)\\\left( P \right) \supset b\\\left( P \right) \cap \left( Q \right) = c\end{array} \right\} \Rightarrow c\parallel b\end{array}\)
Do đó qua \(I\) ta kẻ được hai đường thẳng \(a\) và \(b\) cùng song song với \(c\), mâu thuẫn với định lí qua một điểm nằm ngoài một đường thẳng, có một và chỉ một đường thẳng song song với đường thẳng đó.
Vậy \(c\) phải cắt ít nhất một trong hai đường thẳng \(a,b\).
Nếu đường thẳng \(c\) cắt đường thẳng \(a\) hoặc đường thẳng \(b\), mà đường thẳng \(c\) nằm trong mặt phẳng \(\left( Q \right)\), khi đó đường thẳng \(a\) hoặc đường thẳng \(b\) có 1 điểm chung với mặt phẳng \(\left( Q \right)\). Điều này trái với giả thiết \(a\) và \(b\) cùng song song với \(\left( Q \right)\).
b) Vì \(\left( P \right)\) chứa đường thẳng \(a\) mà \(a\) song song với mặt phẳng \(\left( Q \right)\) nên \(\left( P \right)\) và \(\left( Q \right)\) là hai mặt phẳng phân biệt.
Theo chứng minh ở trên, nếu \(\left( P \right)\) và \(\left( Q \right)\) có điểm chung \(M\) thì mâu thuẫn với giả thiết \(a\) và \(b\) cùng song song với \(\left( Q \right)\).
Vậy hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) không có điểm chung.
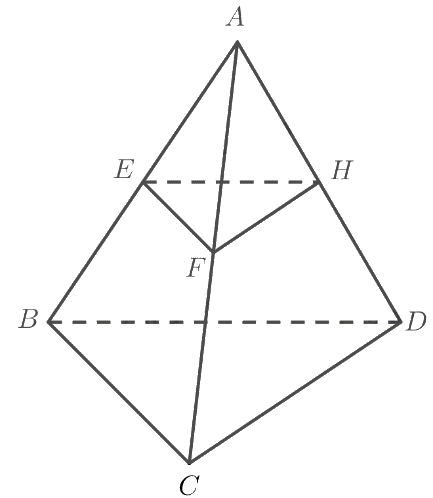
Cho tứ diện \(ABCD\) có \(E,F,H\)lần lượt là trung điểm của \(AB,AC,AD\). Chứng minh \(\left( {EFH} \right)\parallel \left( {BCD} \right)\).
Phương pháp giải:
Sử dụng định lí 1: Nếu mặt phẳng \(\left( P \right)\) chứa hai đường thẳng \(a,b\) cắt nhau và hai đường thẳng đó cùng song song với mặt phẳng \(\left( Q \right)\) thì \(\left( P \right)\) song song với \(\left( Q \right)\).
Lời giải chi tiết:

Ta có: \(E\) là trung điểm của \(AB\)
\(F\) là trung điểm của \(AC\)
\( \Rightarrow EF\) là đường trung bình của tam giác \(ABC\)
\(\left. \begin{array}{l} \Rightarrow EF\parallel BC\\BC \subset \left( {BC{\rm{D}}} \right)\end{array} \right\} \Rightarrow EF\parallel \left( {BC{\rm{D}}} \right)\)
\(E\) là trung điểm của \(AB\)
\(H\) là trung điểm của \(AD\)
\( \Rightarrow EH\) là đường trung bình của tam giác \(ABD\)
\(\left. \begin{array}{l} \Rightarrow EH\parallel BD\\BD \subset \left( {BC{\rm{D}}} \right)\end{array} \right\} \Rightarrow EH\parallel \left( {BC{\rm{D}}} \right)\)
Ta có:
\(\left. \begin{array}{l}EF\parallel \left( {BCD} \right)\\EH\parallel \left( {BCD} \right)\\EF,EH \subset \left( {EFH} \right)\end{array} \right\} \Rightarrow \left( {EFH} \right)\parallel \left( {BCD} \right)\)
Mục 2 của chương trình Toán 11 tập 1 Chân trời sáng tạo tập trung vào các kiến thức về phép biến hình. Cụ thể, các em sẽ được làm quen với các phép biến hình cơ bản như phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các phép biến hình này là nền tảng quan trọng để học tập các kiến thức tiếp theo trong chương trình.
Bài tập mục 2 trang 114, 115 SGK Toán 11 tập 1 Chân trời sáng tạo bao gồm các dạng bài tập khác nhau, yêu cầu học sinh vận dụng kiến thức về các phép biến hình để giải quyết các vấn đề thực tế. Các bài tập này thường xoay quanh việc xác định ảnh của một điểm, một đường thẳng hoặc một hình qua phép biến hình cho trước. Ngoài ra, các em cũng cần phải chứng minh tính chất của các phép biến hình và sử dụng chúng để giải các bài toán hình học.
Ví dụ: Cho điểm A(1; 2) và vectơ v = (3; -1). Tìm tọa độ điểm A' là ảnh của điểm A qua phép tịnh tiến theo vectơ v.
Giải: Tọa độ điểm A' được tính theo công thức: A'(xA + xv; yA + yv) = (1 + 3; 2 - 1) = (4; 1).
Ngoài SGK Toán 11 tập 1 Chân trời sáng tạo, các em có thể tham khảo thêm các tài liệu sau để học tập và ôn luyện:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập mục 2 trang 114, 115 SGK Toán 11 tập 1 Chân trời sáng tạo, các em sẽ hiểu rõ hơn về các phép biến hình và tự tin giải quyết các bài toán liên quan. Chúc các em học tập tốt!