Bài 4 trang 86 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Chân trời sáng tạo. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp tam giác đều (S.ABC) cạnh đáy bằng (2a) và chiều cao bằng (asqrt 2 ).
Đề bài
Cho hình chóp tam giác đều \(S.ABC\) cạnh đáy bằng \(2a\) và chiều cao bằng \(a\sqrt 2 \). Khoảng cách từ tâm \(O\) của đáy \(ABC\) đến một mặt bên là
A. \(\frac{{a\sqrt {14} }}{7}\).
B. \(\frac{{a\sqrt 2 }}{7}\).
C. \(\frac{{a\sqrt {14} }}{2}\).
D. \(\frac{{2a\sqrt {14} }}{7}\).
Phương pháp giải - Xem chi tiết
Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng.
Lời giải chi tiết
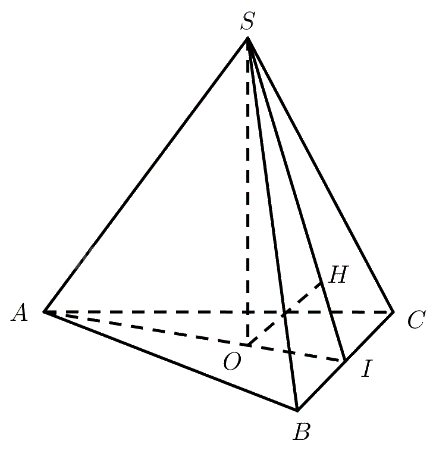
Gọi \(I\) là trung điểm của \(BC\), kẻ \(OH \bot SI\left( {H \in SI} \right)\).
\(ABC\) là tam giác đều \( \Rightarrow AI \bot BC\)
\(SO \bot \left( {ABC} \right) \Rightarrow SO \bot BC\)
\( \Rightarrow BC \bot \left( {SAI} \right) \Rightarrow BC \bot OH\)
Mà \(OH \bot SI\)
\( \Rightarrow OH \bot \left( {SBC} \right) \Rightarrow d\left( {O,\left( {SBC} \right)} \right) = OH\)
\(ABC\) là tam giác đều \( \Rightarrow AI = \frac{{AB\sqrt 3 }}{2} = a\sqrt 3 \Rightarrow OI = \frac{1}{3}AI = \frac{{a\sqrt 3 }}{3}\)
\(SO = a\sqrt 2 \Rightarrow OH = \frac{{SO.OI}}{{\sqrt {S{O^2} + O{I^2}} }} = \frac{{a\sqrt {14} }}{7}\)
Chọn A.
Bài 4 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 4 yêu cầu học sinh xét hàm số f(x) = x3 - 3x2 + 2 và thực hiện các yêu cầu sau:
Để tính đạo hàm f'(x), ta sử dụng quy tắc đạo hàm của hàm số đa thức:
f'(x) = 3x2 - 6x
Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2.
Để xác định xem các điểm này là điểm cực đại hay cực tiểu, ta xét dấu của đạo hàm bậc hai f''(x):
f''(x) = 6x - 6
Tại x = 0, f''(0) = -6 < 0, vậy x = 0 là điểm cực đại.
Tại x = 2, f''(2) = 6 > 0, vậy x = 2 là điểm cực tiểu.
Giá trị của hàm số tại các điểm cực trị là:
Vậy, hàm số có điểm cực đại là (0, 2) và điểm cực tiểu là (2, -2).
Dựa vào dấu của đạo hàm f'(x), ta có thể xác định khoảng đồng biến và nghịch biến của hàm số:
Thông qua việc giải Bài 4 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo, học sinh đã nắm vững kiến thức về đạo hàm, điểm cực trị và khoảng đồng biến, nghịch biến của hàm số. Đây là những kiến thức cơ bản và quan trọng trong chương trình học Toán 11.
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Việc hiểu và vận dụng đạo hàm một cách linh hoạt sẽ giúp học sinh giải quyết các bài toán thực tế một cách hiệu quả.
Để củng cố kiến thức về đạo hàm, học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Ngoài ra, có thể tham khảo các bài giảng trực tuyến và các video hướng dẫn giải bài tập trên giaitoan.edu.vn.
Bài 4 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng, giúp học sinh hiểu sâu hơn về đạo hàm và ứng dụng của nó. Hy vọng với lời giải chi tiết và hướng dẫn trên, học sinh có thể tự tin giải bài tập này và các bài tập tương tự.