Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 4 trang 22, 23 sách giáo khoa Toán 11 tập 1 chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Áp dụng công thức biến đổi tích thành tổng cho hai góc lượng giác (alpha = frac{{alpha + beta }}{2},beta = frac{{alpha - beta }}{2}) ta được đẳng thức nào?
Áp dụng công thức biến đổi tích thành tổng cho hai góc lượng giác \(\alpha = \frac{{\alpha + \beta }}{2},\beta = \frac{{\alpha - \beta }}{2}\) ta được đẳng thức nào?
Phương pháp giải:
Áp dụng công thức:
\(\begin{array}{l}\cos a\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right]\\\sin a\sin b = \frac{1}{2}\left[ {\cos \left( {a - b} \right) - \cos \left( {a + b} \right)} \right]\\\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right]\end{array}\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}\cos \alpha \cos \beta = \cos \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right) + \cos \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \alpha + \cos \beta } \right)\end{array}\)
\(\begin{array}{l}\sin \alpha \sin \beta = \sin \frac{{\alpha + \beta }}{2}\sin \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right) - \cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \beta - \cos \alpha } \right)\end{array}\)
\(\begin{array}{l}\sin \alpha \cos \beta = \sin \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\sin \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right) + \sin \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\sin \alpha + \sin \beta } \right)\end{array}\)
Tính \(\cos \frac{{7\pi }}{{12}} + \cos \frac{\pi }{{12}}\).
Phương pháp giải:
Áp dụng công thức:
\(\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\).
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}\cos \frac{{7\pi }}{{12}} + \cos \frac{\pi }{{12}} = 2\cos \frac{{\frac{{7\pi }}{{12}} + \frac{\pi }{{12}}}}{2}\cos \frac{{\frac{{7\pi }}{{12}} - \frac{\pi }{{12}}}}{2}\\ = 2.\frac{1}{2}.\frac{{\sqrt 2 }}{2} = \frac{{\sqrt 2 }}{2}\end{array}\).
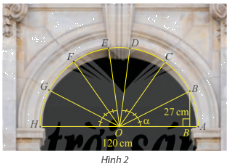
Trong bài toán khởi động, cho biết vòm cổng rộng 120 cm và khoảng cách từ B đến đường kính AH là 27 cm. Tính \(\sin \alpha \) và \(\cos \alpha \), từ đó tính khoảng cách từ điểm C đến đường kính AH. Làm tròn kết quả đến hàng phần mười.
Phương pháp giải:
Quan sát hình vẽ để trả lời.
Lời giải chi tiết:
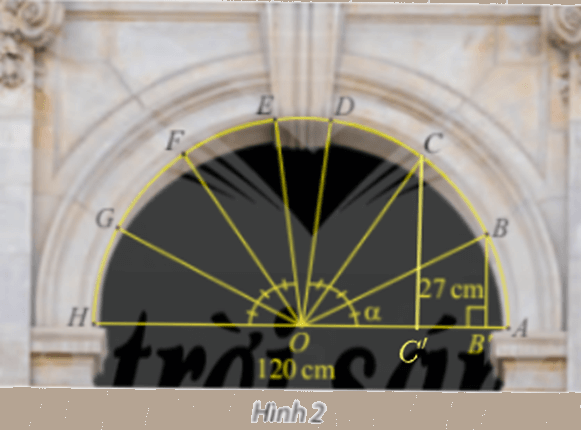
Ta có: \(OA = OB = 120:2 = 60\).
Xét tam giác OBB’ có:
\(\sin \widehat {BOB'} = \frac{{BB'}}{{OB}} = \frac{{27}}{{60}} = \frac{9}{{20}}\).
Ta có: \(\widehat {AOC} = 2\widehat {BOB'}\).
Xét tam giác OCC’ vuông tại C’ có:
\(\begin{array}{l}\sin \widehat {COC'} = \frac{{CC'}}{{OC}}\\ \Leftrightarrow CC' = OC.\sin \widehat {COC'} = OC.\sin \left( {2\widehat {BOB'}} \right)\end{array}\).
Mà \(\sin \left( {2\widehat {BOB'}} \right) = 2.\sin \widehat {BOB'}.cos\widehat {BOB'}\).
\( = 2.\frac{9}{{20}}.\frac{{\sqrt {319} }}{{20}} = \frac{{9\sqrt {319} }}{{400}}\).
Vậy khoảng cách từ C đến AH là \(60.\frac{{9\sqrt {319} }}{{200}} \approx 48,2cm\).
Mục 4 của chương trình Toán 11 tập 1 Chân trời sáng tạo tập trung vào các kiến thức về vectơ trong không gian. Cụ thể, các em sẽ được làm quen với các khái niệm như:
Cho hai vectơ \vec{a} = (1; -2; 3) và \vec{b} = (-2; 1; 0). Tính:
Lời giải:
Cho hai vectơ \vec{u} = (2; -1; 1) và \vec{v} = (1; 0; -2). Tính tích vô hướng \vec{u} \cdot \vec{v}.
Lời giải:
\vec{u} \cdot \vec{v} = (2)(1) + (-1)(0) + (1)(-2) = 2 + 0 - 2 = 0
Kiến thức về vectơ trong không gian có ứng dụng rất lớn trong nhiều lĩnh vực khác nhau, bao gồm:
Hy vọng với lời giải chi tiết và những chia sẻ trên, các em sẽ hiểu rõ hơn về mục 4 trang 22, 23 SGK Toán 11 tập 1 Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao!