Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 4 trang 83, 84 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập trong mục này tập trung vào các kiến thức về...
Cho hai hàm số \(y = f\left( x \right) = \frac{1}{{x - 1}}\) và \(y = g\left( x \right) = \sqrt {4 - x} \).
Cho hai hàm số \(y = f\left( x \right) = \frac{1}{{x - 1}}\) và \(y = g\left( x \right) = \sqrt {4 - x} \).
Hàm số \(y = f\left( x \right) + g\left( x \right)\) có liên tục tại \(x = 2\) không? Giải thích.
Phương pháp giải:
Xét tính liên tục của hàm số \(h\left( x \right) = f\left( x \right) + g\left( x \right)\) tại \(x = 2\):
Bước 1: Kiểm tra x = 2 có thuộc tập xác định không. Tính \(h\left( 2 \right)\).
Bước 2: Tính \(\mathop {\lim }\limits_{x \to 2} h\left( x \right)\).
Bước 3: Kết luận.
Lời giải chi tiết:
Đặt \(h\left( x \right) = f\left( x \right) + g\left( x \right) = \frac{1}{{x - 1}} + \sqrt {4 - x} \). Ta có:
\(\begin{array}{l}h\left( 2 \right) = \frac{1}{{2 - 1}} + \sqrt {4 - 2} = 1 + \sqrt 2 \\\mathop {\lim }\limits_{x \to 2} h\left( x \right) = \mathop {\lim }\limits_{x \to x} \left( {\frac{1}{{x - 1}} + \sqrt {4 - x} } \right) = \frac{1}{{2 - 1}} + \sqrt {4 - 2} = 1 + \sqrt 2 \end{array}\)
Vì \(\mathop {\lim }\limits_{x \to 2} h\left( x \right) = h\left( 2 \right)\) nên hàm số \(y = f\left( x \right) + g\left( x \right)\) liên tục tại \(x = 2\).
Xét tính liên tục của các hàm số:
a) \(y = \sqrt {{x^2} + 1} + 3 - x\);
b) \(y = \frac{{{x^2} - 1}}{x}.\cos x\).
Phương pháp giải:
Đưa hàm số thành tổng, hiệu, tích của hai hàm số rồi xét tính liên tục của hai hàm số đó.
Lời giải chi tiết:
a) TXĐ: \(D = \mathbb{R}\)
Hàm số \(y = \sqrt {{x^2} + 1} \) xác định trên \(\mathbb{R}\) nên liên tục trên \(\mathbb{R}\).
Hàm số \(y = 3 - x\) là đa thức nên liên tục trên \(\mathbb{R}\).
Vậy hàm số \(y = \sqrt {{x^2} + 1} + 3 - x\) cũng liên tục trên \(\mathbb{R}\).
b) TXĐ: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
Hàm số \(y = \frac{{{x^2} - 1}}{x}\) là hàm phân thức hữu tỉ nên liên tục trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).
Hàm số \(y = \cos x\) là hàm lượng giác nên liên tục trên \(\mathbb{R}\). Vậy hàm số \(y = \cos x\) cũng liên tục trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).
Vậy hàm số \(y = \frac{{{x^2} - 1}}{x}.\cos x\) liên tục trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).
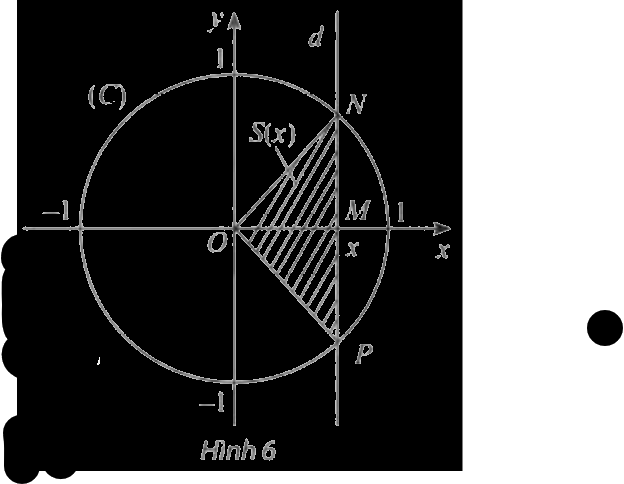
Trong mặt phẳng toạ độ \(Oxy\), cho đường tròn \(\left( C \right)\) tâm \(O\), bán kính bằng 1. Một đường thẳng \(d\) thay đổi, luôn vuông góc với trục hoành, cắt trục hoành tại điểm \(M\) có hoành độ \(x\left( { - 1 < x < 1} \right)\) và cắt đường tròn \(\left( C \right)\) tại các điểm \(N\) và \(P\) (xem Hình 6).
a) Viết biểu thức \(S\left( x \right)\) biểu thị diện tích của tam giác \(ONP\).
b) Hàm số \(y = S\left( x \right)\) có liên tục trên \(\left( { - 1;1} \right)\) không? Giải thích.
c) Tìm các giới hạn \(\mathop {\lim }\limits_{x \to {1^ - }} S\left( x \right)\) và \(\mathop {\lim }\limits_{x \to - {1^ + }} S\left( x \right)\).
Phương pháp giải:
a) Viết hàm số biểu thị phương trình đường tròn \(\left( C \right)\), dựa vào dữ kiện của đề bài, tính \(OM,NP\) sau đó tính diện tích \(S\left( x \right)\) của tam giác \(ONP\).
b) Sử dụng tính chất liên tục của các hàm số sơ cấp.
c) Áp dụng các công thức tính giới hạn của hàm số.
Lời giải chi tiết:
a) Ta có: \(\left( C \right):{x^2} + {y^2} = 1 \Leftrightarrow y = \pm \sqrt {1 - {x^2}} \).
Độ dài \(OM\) chính là giá trị tuyệt đối của hoành độ của điểm \(M\). Vậy \(OM = \left| x \right|\).
Độ dài \(MN\) chính là giá trị tuyệt đối của tung độ của điểm \(N\). Vậy \(MN = \left| {\sqrt {1 - {x^2}} } \right| = \sqrt {1 - {x^2}} \).
\(S\left( x \right) = {S_{ONP}} = \frac{1}{2}.NP.OM = MN.OM = \sqrt {1 - {x^2}} .\left| x \right|\).
b) Xét hàm số \(S\left( x \right) = \sqrt {1 - {x^2}} .\left| x \right| = \left\{ {\begin{array}{*{20}{c}}{x\sqrt {1 - {x^2}} }&{khi\,\,0 \le x \le 1}\\{ - x\sqrt {1 - {x^2}} }&{khi\,\, - 1 \le x < 0}\end{array}} \right.\).
ĐKXĐ: \(1 - {x^2} \ge 0 \Leftrightarrow - 1 \le x \le 1\)
Hàm số \(S\left( x \right)\) có tập xác định là \(\left[ { - 1;1} \right]\).
Vậy hàm số \(S\left( x \right)\) xác định trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {0;1} \right)\) nên liên tục trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {0;1} \right)\).
Ta có: \(S\left( 0 \right) = 0.\sqrt {1 - {0^2}} = 0\)
\(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {x\sqrt {1 - {x^2}} } \right) = 0.\sqrt {1 - {0^2}} = 0\)
\(\mathop {\lim }\limits_{x \to {0^ - }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( { - x\sqrt {1 - {x^2}} } \right) = - 0.\sqrt {1 - {0^2}} = 0\)
Vì \(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} S\left( x \right) = 0\) nên \(\mathop {\lim }\limits_{x \to 0} S\left( x \right) = 0 = S\left( 0 \right)\)
Vậy hàm số \(S\left( x \right)\) liên tục tại điểm \({x_0} = 0\). Vậy hàm số \(S\left( x \right)\) liên tục trên \(\left( { - 1;1} \right)\).
c) \(\mathop {\lim }\limits_{x \to {1^ - }} S\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( {x\sqrt {1 - {x^2}} } \right) = 1.\sqrt {1 - {1^2}} = 0\)
\(\mathop {\lim }\limits_{x \to - {1^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \left( { - x\sqrt {1 - {x^2}} } \right) = - 1.\sqrt {1 - {{\left( { - 1} \right)}^2}} = 0\)
Mục 4 của SGK Toán 11 tập 1 chương trình Chân trời sáng tạo tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc hai. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 1: (Trang 83) Tìm tập xác định của các hàm số sau:
Lời giải:
Bài 2: (Trang 84) Xác định parabol y = ax² + bx + c trong mỗi trường hợp sau:
Lời giải:
Để giải nhanh các bài tập về hàm số bậc hai, các em cần nắm vững các kiến thức cơ bản về hàm số bậc hai, bao gồm:
Ngoài ra, các em cũng cần luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau và rèn luyện kỹ năng giải bài tập một cách nhanh chóng và chính xác.
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, các em học sinh đã có thể tự tin hơn trong việc giải các bài tập mục 4 trang 83, 84 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo. Chúc các em học tập tốt!