Bài 6 trang 12 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc ôn tập chương 1: Hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về các loại hàm số, tính đơn điệu, cực trị và ứng dụng của đạo hàm để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Trong Hình 15, mâm bánh xe ô tô được chia thành năm phần bằng nhau. Viết công thức số đo tổng quát của góc lượng giác (Ox; ON).
Đề bài
Trong Hình 15, mâm bánh xe ô tô được chia thành năm phần bằng nhau. Viết công thức số đo tổng quát của góc lượng giác (Ox; ON).
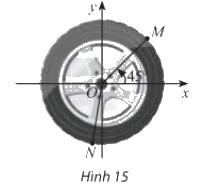
Phương pháp giải - Xem chi tiết
Sử dụng công thức số đo tổng quát của góc lượng giác.
Lời giải chi tiết
Vì mâm bánh xe ô tô được chia thành năm phần bằng nhau nên một phần có số đo là \(\frac{{{{360}^ \circ }}}{5} = {72^ \circ }\)
Ta có
\[\begin{array}{l}\left( {ON;{\rm{ }}OM} \right) = \left( {ON;{\rm{ }}Ox} \right) + \left( {Ox;{\rm{ }}OM} \right)\\\,\,\,\,\,\,\,{2.72^ \circ }\,\,\,\,\,\,\, = \,\left( {ON;{\rm{ }}Ox} \right)\, + \,\,\,\,\,\,\,{45^ \circ }\\ \Rightarrow \left( {ON;{\rm{ }}Ox} \right) = {99^ \circ }\end{array}\]
Công thức số đo tổng quát của góc lượng giác \[\left( {ON;{\rm{ }}Ox} \right) = {99^ \circ } + k{.360^ \circ }\,\,(k \in Z)\]
Bài 6 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về hàm số và ứng dụng của đạo hàm. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 6 yêu cầu học sinh xét hàm số f(x) = x3 - 3x2 + 2 và thực hiện các yêu cầu sau:
Xác định tập xác định của hàm số.
Tính đạo hàm f'(x).
Tìm các điểm cực trị của hàm số.
Khảo sát sự biến thiên của hàm số.
Vẽ đồ thị hàm số.
1. Tập xác định:
Hàm số f(x) = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là D = ℝ.
2. Đạo hàm:
f'(x) = 3x2 - 6x
3. Tìm điểm cực trị:
Để tìm điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2.
Ta xét dấu của f'(x) trên các khoảng xác định:
Khi x < 0, f'(x) > 0, hàm số đồng biến.
Khi 0 < x < 2, f'(x) < 0, hàm số nghịch biến.
Khi x > 2, f'(x) > 0, hàm số đồng biến.
Vậy, hàm số đạt cực đại tại x = 0, f(0) = 2 và đạt cực tiểu tại x = 2, f(2) = -2.
4. Khảo sát sự biến thiên:
Hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞).
Hàm số nghịch biến trên khoảng (0; 2).
Hàm số đạt cực đại tại x = 0, giá trị cực đại là 2.
Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là -2.
5. Vẽ đồ thị:
Dựa vào các thông tin đã khảo sát, ta có thể vẽ đồ thị hàm số f(x) = x3 - 3x2 + 2.
Khi giải bài tập về hàm số, cần chú ý các bước sau:
Xác định đúng tập xác định của hàm số.
Tính đạo hàm chính xác.
Giải phương trình đạo hàm bằng 0 để tìm điểm cực trị.
Khảo sát sự biến thiên của hàm số bằng cách xét dấu đạo hàm.
Vẽ đồ thị hàm số một cách chính xác.
Việc nắm vững các kiến thức về hàm số và đạo hàm là rất quan trọng để giải quyết các bài tập trong chương trình Toán 11. Hãy luyện tập thường xuyên để nâng cao kỹ năng giải toán của bạn.
Hy vọng lời giải chi tiết này sẽ giúp bạn hiểu rõ hơn về Bài 6 trang 12 SGK Toán 11 tập 1 - Chân trời sáng tạo. Chúc bạn học tập tốt!