Chào mừng các em học sinh đến với lời giải chi tiết Bài 2 trang 99 SGK Toán 11 tập 1 - Chân trời sáng tạo. Bài học này thuộc chương trình học Toán 11, tập trung vào việc vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp lời giải chính xác, dễ hiểu và phương pháp giải bài tập hiệu quả.
Cho hình chóp (S.ABCD) có đáy là hình bình hành. Gọi (M) là trung điểm của (SC).
Đề bài
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M\) là trung điểm của \(SC\).
a) Tìm giao điểm \(I\) của đường thẳng \(AM\) và mặt phẳng \(\left( {SBD} \right)\). Chứng minh \(IA = 2IM\).
b) Tìm giao điểm \(E\) của đường thẳng \(S{\rm{D}}\) và mặt phẳng \(\left( {ABM} \right)\).
c) Gọi \(N\) là một điểm tuỳ ý trên cạnh \(AB\). Tìm giao điểm của đường thẳng \(MN\) và mặt phẳng \(\left( {SBD} \right)\).
Phương pháp giải - Xem chi tiết
‒ Để tìm giao điểm của đường thẳng và mặt phẳng, ta tìm giao điểm của đường thẳng đó với một đường thẳng trong mặt phẳng.
‒ Để chứng minh \(IA = 2IM\), ta dựa vào tính chất trọng tâm của tam giác.
Lời giải chi tiết
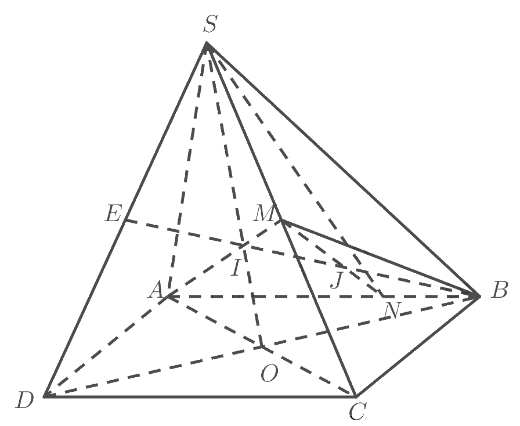
a) Gọi \(O\) là giao điểm của \(AC\) và \(BD\).
Trong mặt phẳng \((SAC)\), gọi \(I\) là giao điểm của \(AM\) và \(SO\). Ta có:
\(\left. \begin{array}{l}I \in SO \subset \left( {SB{\rm{D}}} \right)\\I \in AM\end{array} \right\} \Rightarrow I = AM \cap \left( {SB{\rm{D}}} \right)\)
Xét tam giác \(SAC\) có:
\(ABCD\) là hình bình hành \( \Rightarrow O\) là trung điểm của \(AC\) \( \Rightarrow SO\) là trung truyến của tam giác \(SAC\).
Theo đề bài ta có \(M\) là trung điểm của \(SC\) \( \Rightarrow AM\) là trung truyến của tam giác \(SAC\).
Mà \(I = SO \cap AM\)
\( \Rightarrow I\) là trọng tâm của tam giác SAC suy ra IA = 2IM.
b) Trong mặt phẳng \((SBD)\), gọi \(E\) là giao điểm của \(S{\rm{D}}\) và \(BI\). Ta có:
\(\left. \begin{array}{l}E \in BI \subset \left( {ABM} \right)\\E \in S{\rm{D}}\end{array} \right\} \Rightarrow E = S{\rm{D}} \cap \left( {ABM} \right)\)
c) Mặt phẳng (ABM) chứa BE, MN. Gọi \(J\) là giao điểm của \(MN\) và \(BE\). Ta có:
\(\left. \begin{array}{l}J \in BE \subset \left( {SB{\rm{D}}} \right)\\J \in MN\end{array} \right\} \Rightarrow J = MN \cap \left( {SB{\rm{D}}} \right)\)
Bài 2 trang 99 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về hàm số và đồ thị để giải quyết. Dưới đây là lời giải chi tiết và hướng dẫn từng bước để các em có thể hiểu rõ hơn về bài toán này.
Bài 2 yêu cầu học sinh thực hiện các thao tác sau:
Để giải bài 2 trang 99 SGK Toán 11 tập 1 - Chân trời sáng tạo, chúng ta cần thực hiện các bước sau:
Giả sử hàm số cần xét là y = x3 - 3x2 + 2. Chúng ta sẽ thực hiện các bước trên để giải bài toán.
Bước 1: Tập xác định của hàm số là R.
Bước 2: Đạo hàm của hàm số là y' = 3x2 - 6x.
Bước 3: Giải phương trình y' = 0, ta được x = 0 hoặc x = 2. Vậy hàm số có hai điểm cực trị là x = 0 và x = 2.
Bước 4: Lập bảng biến thiên:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Bước 5: Dựa vào bảng biến thiên, ta có thể vẽ được đồ thị hàm số.
Khi giải bài 2 trang 99 SGK Toán 11 tập 1 - Chân trời sáng tạo, các em cần chú ý:
Bài 2 trang 99 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp các em củng cố kiến thức về hàm số và đồ thị. Hy vọng với lời giải chi tiết và hướng dẫn trên, các em sẽ hiểu rõ hơn về bài toán này và tự tin giải quyết các bài tập tương tự.
giaitoan.edu.vn luôn sẵn sàng hỗ trợ các em trong quá trình học tập. Chúc các em học tốt!