Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 94, 95 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập mục 3 tập trung vào các kiến thức quan trọng về...
Cho đường thẳng \(a\) và điểm \(A\) không nằm trên \(a\). Trên \(a\) lấy hai điểm \(B,C\). Đường thẳng \(a\) có nằm trong mặt phẳng \(\left( {ABC} \right)\) không? Giải thích.
Cho đường thẳng \(a\) và điểm \(A\) không nằm trên \(a\). Trên \(a\) lấy hai điểm \(B,C\). Đường thẳng \(a\) có nằm trong mặt phẳng \(\left( {ABC} \right)\) không? Giải thích.
Phương pháp giải:
Áp dụng các tính chất:
‒ Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
‒ Tính chất 3: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
Lời giải chi tiết:
Áp dụng tính chất 2, ta có duy nhất một mặt phẳng đi qua ba điểm phân biệt \(A,B,C\) là mặt phẳng \(\left( {ABC} \right)\).
Áp dụng tính chất 3, ta có đường thẳng \(a\) có hai điểm phân biệt \(B,C\) nằm trong mặt phẳng \(\left( {ABC} \right)\) nên mọi điểm của đường thẳng \(a\) cũng nằm trong mặt phẳng \(\left( {ABC} \right)\). Vậy đường thẳng \(a\) nằm trong mặt phẳng \(\left( {ABC} \right)\).
Hai đường thẳng phân biệt \(a\) và \(b\) cắt nhau tại điểm \(O\). Trên \(a,b\) lấy lần lượt hai điểm \(M,N\) khác \(O\). Gọi \(\left( P \right)\) là mặt phẳng đi qua ba điểm \(M,N,O\) (Hình 25). Mặt phẳng \(\left( P \right)\) có chứa cả hai đường thẳng \(a\) và \(b\) không? Giải thích.
Phương pháp giải:
Áp dụng các tính chất:
‒ Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
‒ Tính chất 3: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
Lời giải chi tiết:
Áp dụng tính chất 2, ta có \(\left( P \right)\) là mặt phẳng duy nhất đi qua ba điểm phân biệt \(A,B,C\) là mặt phẳng \(M,N,O\).
Áp dụng tính chất 3, ta có
– Đường thẳng \(a\) có hai điểm phân biệt \(M,O\) nằm trong mặt phẳng \(\left( P \right)\) nên mọi điểm của đường thẳng \(a\) cũng nằm trong mặt phẳng \(\left( P \right)\). Vậy đường thẳng \(a\) nằm trong mặt phẳng \(\left( P \right)\).
– Đường thẳng \(b\) có hai điểm phân biệt \(N,O\) nằm trong mặt phẳng \(\left( P \right)\) nên mọi điểm của đường thẳng \(b\) cũng nằm trong mặt phẳng \(\left( P \right)\). Vậy đường thẳng \(b\) nằm trong mặt phẳng \(\left( P \right)\).
Cho hai đường thẳng \(a\) và \(b\) cắt nhau tại \(O\) và điểm \(M\) không thuộc \(mp\left( {a,b} \right)\).
a) Tìm giao tuyến của hai mặt phẳng \(\left( {M,a} \right)\) và \(\left( {M,b} \right)\).
b) Lấy \(A,B\) lần lượt là hai điểm trên \(a,b\) và khác với điểm \(O\). Tìm giao tuyến của \(\left( {MAB} \right)\) và \(mp\left( {a,b} \right)\).
c) Lấy điểm \(A'\) trên đoạn \(MA\) và điểm \(B'\) trên đoạn \(MB\) sao cho đường thẳng \(A'B'\) cắt \(mp\left( {a,b} \right)\) tại \(C\). Chứng minh ba điểm \(A,B,C\) thẳng hàng.
Phương pháp giải:
‒ Để tìm giao tuyến của hai mặt phẳng, ta tìm hai điểm chung phân biệt của hai mặt phẳng đó.
‒ Để chứng minh ba điểm thẳng hàng, ta chứng minh ba điểm đó cùng thuộc giao tuyến của hai mặt phẳng.
Lời giải chi tiết:
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}M \in \left( {M,a} \right)\\M \in \left( {M,b} \right)\end{array} \right\} \Rightarrow M \in \left( {M,a} \right) \cap \left( {M,b} \right)\\\left. \begin{array}{l}O \in a \subset \left( {M,a} \right)\\O \in b \subset \left( {M,b} \right)\end{array} \right\} \Rightarrow O \in \left( {M,a} \right) \cap \left( {M,b} \right)\end{array}\)
Vậy giao tuyến của hai mặt phẳng \(\left( {M,a} \right)\) và \(\left( {M,b} \right)\) là đường thẳng \(MO\).
b) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}A \in \left( {MAB} \right)\\A \in a \subset \left( {a,b} \right)\end{array} \right\} \Rightarrow A \in \left( {MAB} \right) \cap \left( {a,b} \right)\\\left. \begin{array}{l}B \in \left( {MAB} \right)\\B \in b \subset \left( {a,b} \right)\end{array} \right\} \Rightarrow B \in \left( {MAB} \right) \cap \left( {a,b} \right)\end{array}\)
Vậy giao tuyến của hai mặt phẳng \(\left( {MAB} \right)\) và \(\left( {a,b} \right)\) là đường thẳng \(AB\) (1).
c) Ta có:
\(\left. \begin{array}{l}A' \in MA \subset \left( {MAB} \right)\\B' \in MB \subset \left( {MAB} \right)\end{array} \right\} \Rightarrow A'B' \subset \left( {MAB} \right)\)
Vì \(C \in A'B' \subset \left( {MAB} \right)\) và \(C \in mp\left( {a,b} \right)\) nên điểm \(C\) nằm trên giao tuyến của hai mặt phẳng \(\left( {MAB} \right)\) và \(\left( {a,b} \right)\) (2).
Từ (1) và (2) suy ra ba điểm \(A,B,C\) thẳng hàng.
Giải thích tại sao ghế bốn chân có thể bị khập khiễng còn ghế ba chân thì không.
Phương pháp giải:
Áp dụng các tính chất:
‒ Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
‒ Tính chất 4: Tồn tại bốn điểm không cùng nằm trên một mặt phẳng.
Lời giải chi tiết:
‒ Với ghế 4 chân, nếu 4 điểm tại chân ghế không thuộc một mặt phẳng thì ghế có thể bị khập khiễng.
‒ Với ghế 3 chân, ta chỉ xác định được duy nhất một mặt phẳng đi qua 3 điểm thuộc chân ghế nên ghế ba chân không thể khập khiễng.
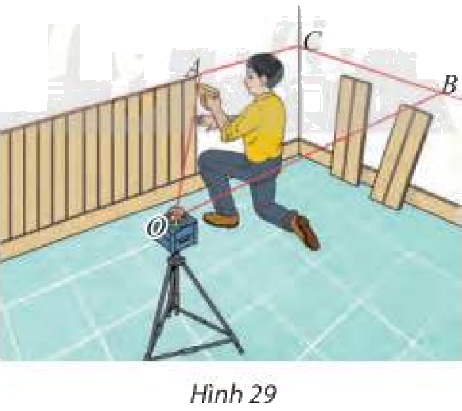
Trong xây dựng, người ta thường dùng máy quét tia laser để kẻ các đường thẳng trên tường hoặc sàn nhà. Tìm giao tuyến của mặt phẳng tạo bởi các tia laser \(OA\) và \(OB\) với các mặt tường trong Hình 29.

Phương pháp giải:
Quan sát hình ảnh và trả lời câu hỏi.
Lời giải chi tiết:
Từ Hình 29 ta thấy: Giao tuyến của mặt phẳng tạo bởi các tia laser \(OA\) và \(OB\) với các mặt tường là \(AC\) và \(BC\).
Mục 3 trang 94, 95 SGK Toán 11 tập 1 Chân trời sáng tạo là một phần quan trọng trong chương trình học, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế. Để giúp các em học sinh hiểu rõ hơn về nội dung này, giaitoan.edu.vn xin trình bày chi tiết lời giải của từng bài tập, kèm theo phương pháp giải và các lưu ý quan trọng.
Mục 3 thường bao gồm các dạng bài tập liên quan đến... (Ví dụ: hàm số, đạo hàm, giới hạn, phương trình, bất phương trình, hình học...). Các bài tập này đòi hỏi học sinh phải nắm vững các định nghĩa, tính chất, công thức và phương pháp giải đã được học trong chương trình.
Đề bài: (Nêu đề bài cụ thể)
Lời giải: (Giải chi tiết bài tập, trình bày các bước giải rõ ràng, dễ hiểu)
Lưu ý: (Các lưu ý quan trọng khi giải bài tập)
Đề bài: (Nêu đề bài cụ thể)
Lời giải: (Giải chi tiết bài tập, trình bày các bước giải rõ ràng, dễ hiểu)
Lưu ý: (Các lưu ý quan trọng khi giải bài tập)
Đề bài: (Nêu đề bài cụ thể)
Lời giải: (Giải chi tiết bài tập, trình bày các bước giải rõ ràng, dễ hiểu)
Lưu ý: (Các lưu ý quan trọng khi giải bài tập)
(Giải một bài tập khó, trình bày chi tiết các bước giải và giải thích rõ ràng)
Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập trong Mục 3 trang 94, 95 SGK Toán 11 tập 1 Chân trời sáng tạo, các em học sinh sẽ hiểu rõ hơn về nội dung này và tự tin hơn trong quá trình học tập. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất.
| Bài tập | Lời giải | Lưu ý |
|---|---|---|
| Bài 1 | (Tóm tắt lời giải) | (Tóm tắt lưu ý) |
| Bài 2 | (Tóm tắt lời giải) | (Tóm tắt lưu ý) |
| Bài 3 | (Tóm tắt lời giải) | (Tóm tắt lưu ý) |