Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 82, 83 SGK Toán 11 tập 2 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học và hiệu quả.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 11 và đạt kết quả cao trong học tập.
Cho đường thẳng (a) và mặt phẳng (left( P right)).
Cho đường thẳng \(a\) và mặt phẳng \(\left( P \right)\).
a) Trong trường hợp \(a\) vuông góc với \(\left( P \right)\), tìm góc giữa \(a\) và một đường thẳng \(b\) tuỳ ý trong \(\left( P \right)\).
b) Trong trường hợp \(a\) không vuông góc với \(\left( P \right)\), tìm góc giữa \(a\) và đường thẳng \(a'\) là hình chiếu vuông góc của \(a\) trên \(\left( P \right)\).
Phương pháp giải:
Sử dụng tính chất: Đường thẳng vuông góc với mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng.
Lời giải chi tiết:
a) Ta có:
\(\left. \begin{array}{l}a \bot \left( P \right)\\b \subset \left( P \right)\end{array} \right\} \Rightarrow a \bot b \Rightarrow \left( {a,b} \right) = {90^ \circ }\)
b) Lấy \(A \in a\). Gọi \(O = a \cap \left( P \right)\). Dựng \(AH \bot a'\left( {H \in a'} \right)\).
Ta có: \(\left( {a,a'} \right) = \left( {AO,OH} \right) = \widehat {AOH}\)
Cho hình lập phương \(ABCD.A'B'C'D'\). Tính góc giữa các đường thẳng sau đây với mặt phẳng \(\left( {ABCD} \right)\):
a) \(AA'\);
b) \(BC'\);
c) \(A'C\).
Phương pháp giải:
Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
Lời giải chi tiết:

a) \(AA' \bot \left( {ABCD} \right) \Rightarrow \left( {AA',\left( {ABCD} \right)} \right) = {90^ \circ }\).
b) \(CC' \bot \left( {ABCD} \right)\)
\( \Rightarrow \left( {BC',\left( {ABCD} \right)} \right) = \left( {BC',BC} \right) = \widehat {CBC'} = {45^ \circ }\)
c) \(AA' \bot \left( {ABCD} \right)\)
\( \Rightarrow \left( {A'C,\left( {ABCD} \right)} \right) = \left( {A'C,AC} \right) = \widehat {ACA'}\)
\(\begin{array}{l}AC = AB\sqrt 2 = AA'\sqrt 2 \Rightarrow \tan \widehat {ACA'} = \frac{{AA'}}{{AC}} = \frac{{AA'}}{{AA'\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\\ \Rightarrow \widehat {ACA'} \approx 35,{26^ \circ }\end{array}\)
Vậy \(\left( {A'C,\left( {ABCD} \right)} \right) \approx 35,{26^ \circ }\)
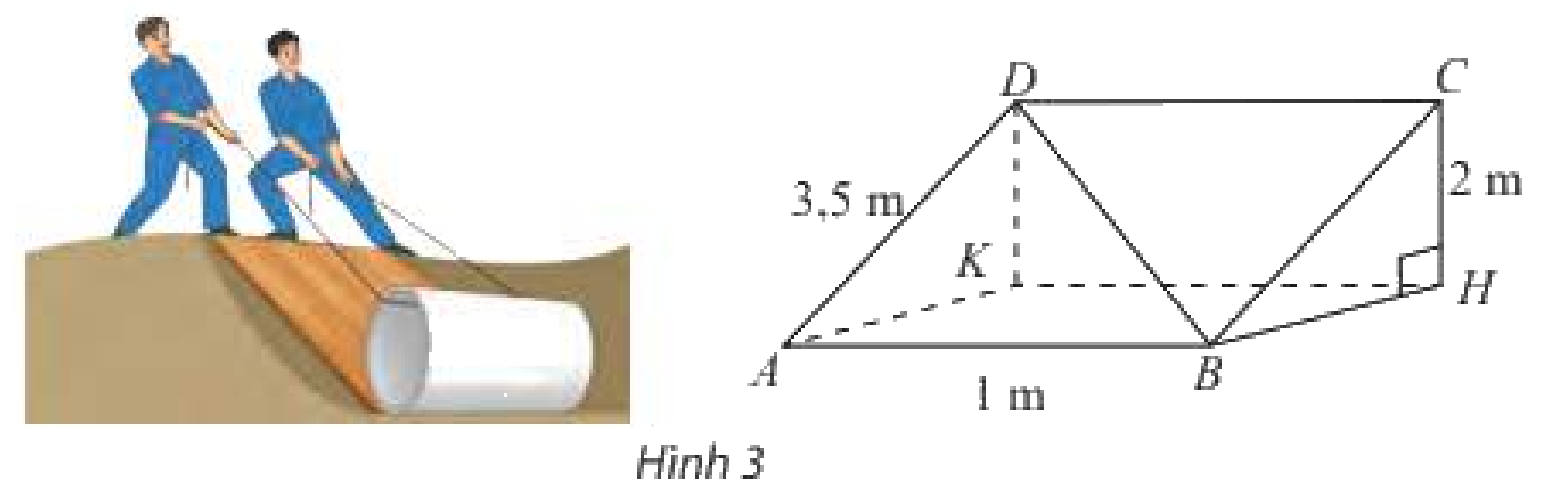
Một tấm ván hình chữ nhật \(ABCD\) được dùng làm mặt phẳng nghiêng để kéo một vật lên khỏi hố sâu 2 m. Cho biết \(AB = 1\,m,AD = 3,5{\rm{ }}m\). Tính góc giữa đường thẳng \(BD\) và đáy hồ.

Phương pháp giải:
Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
Lời giải chi tiết:
\(DK \bot \left( {ABHK} \right) \Rightarrow \left( {B{\rm{D}},\left( {ABHK} \right)} \right) = \left( {B{\rm{D}},BK} \right) = \widehat {DBK}\)
\(DK = CH = 2,AK = \sqrt {A{{\rm{D}}^2} - D{K^2}} = \frac{{\sqrt {33} }}{2},KB = \sqrt {A{K^2} + A{B^2}} = \frac{{\sqrt {37} }}{2}\)
\(\tan \widehat {DBK} = \frac{{DK}}{{KB}} = \frac{4}{{\sqrt {37} }} \Rightarrow \widehat {DBK} \approx 33,{3^ \circ }\)
Vậy góc giữa đường thẳng \(BD\) và đáy hồ bằng \(33,{3^ \circ }\).
Mục 1 của chương trình Toán 11 tập 2 Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, ví dụ như phép biến hình, hàm số lượng giác, hoặc các ứng dụng của đạo hàm. Việc nắm vững kiến thức nền tảng và phương pháp giải bài tập trong mục này là vô cùng quan trọng để các em có thể tiếp thu các kiến thức nâng cao hơn trong chương trình học.
Để giúp các em hiểu rõ hơn về nội dung bài tập, chúng ta sẽ cùng nhau phân tích từng bài tập cụ thể trong mục 1 trang 82, 83 SGK Toán 11 tập 2 Chân trời sáng tạo.
Bài tập này yêu cầu các em vận dụng kiến thức về... để giải quyết. Lời giải chi tiết như sau:
Lưu ý: Các em cần chú ý đến các điều kiện của bài toán và kiểm tra lại kết quả sau khi giải xong.
Bài tập này tập trung vào việc... Để giải bài tập này, các em có thể sử dụng phương pháp...
Trong mục 1 trang 82, 83 SGK Toán 11 tập 2 Chân trời sáng tạo, các em có thể gặp các dạng bài tập sau:
Để giải bài tập Toán 11 tập 2 Chân trời sáng tạo một cách hiệu quả, các em có thể tham khảo một số mẹo sau:
Kiến thức trong mục 1 trang 82, 83 SGK Toán 11 tập 2 Chân trời sáng tạo có ứng dụng rất lớn trong thực tế, ví dụ như...
Hy vọng rằng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ tự tin hơn trong việc học tập môn Toán 11 tập 2 Chân trời sáng tạo. Chúc các em học tốt!
| Bài tập | Lời giải |
|---|---|
| Bài 1 | (Lời giải chi tiết bài 1) |
| Bài 2 | (Lời giải chi tiết bài 2) |