Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 13, 14, 15 sách giáo khoa Toán 11 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác (frac{{2pi
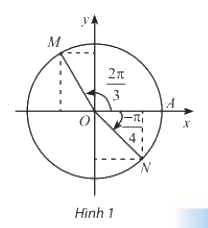
Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác \(\frac{{2\pi }}{3}\) và \(\frac{\pi }{4}\) trên
đường tròn lượng giác. Xác định tọa độ của M và N trong hệ trục tọa độ Oxy .
Phương pháp giải:
Dựa vào kiến thức đã học để xác định
Lời giải chi tiết:
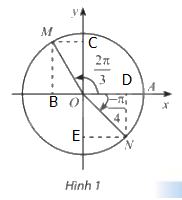
Gọi B, C lần lượt là hình chiếu của M lên Ox, Oy
D,E lần lượt là hình chiếu của N lên Ox, Oy
Ta có OM = ON = 1
\(\widehat {MOC} = \frac{{2\pi }}{3} - \frac{\pi }{2} = \frac{\pi }{6} \Rightarrow \left\{ \begin{array}{l}\sin \widehat {MOC} = \frac{1}{2} = \frac{{MC}}{{OM}} \Rightarrow MC = \frac{1}{2}\\\cos \widehat {MOC} = \frac{{\sqrt 3 }}{2} = \frac{{MB}}{{OM}} \Rightarrow MB = \frac{{\sqrt 3 }}{2}\end{array} \right.\)
Do điểm M có hoành độ nằm bên trái trục Ox nên tọa độ của điểm M \(\left( {\frac{-1}{2};\frac{{\sqrt 3 }}{2}} \right)\)
\(\widehat {NOD} = - \frac{\pi }{4} \Rightarrow \left\{ \begin{array}{l}\sin \widehat {NOD} = - \frac{{\sqrt 2 }}{2} = \frac{{ND}}{{ON}} \Rightarrow ND = - \frac{{\sqrt 2 }}{2}\\\cos \widehat {NOD} = \frac{{\sqrt 2 }}{2} = \frac{{NE}}{{ON}} \Rightarrow NE = \frac{{\sqrt 2 }}{2}\end{array} \right.\)
Tọa độ của điểm N \(\left( { \frac{{\sqrt 2 }}{2};\frac{-{\sqrt 2 }}{2}} \right)\)
Tính \(\sin \left( { - \frac{{2\pi }}{3}} \right)\) và \(\tan 495^\circ \)
Phương pháp giải:
Dựa vào kiến thức đã học ở phần trên để tính
Lời giải chi tiết:
\(\begin{array}{l}\sin \left( { - \frac{{2\pi }}{3}} \right) = - \frac{{\sqrt 3 }}{2}\\\tan 495^\circ = - 1\end{array}\)
Mục 1 của chương trình Toán 11 tập 1 - Chân trời sáng tạo tập trung vào việc giới thiệu về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng, mở đầu cho chương trình Giải tích. Việc hiểu rõ về giới hạn sẽ giúp học sinh tiếp cận các khái niệm phức tạp hơn như đạo hàm và tích phân một cách dễ dàng hơn.
Mục 1 bao gồm các nội dung chính sau:
Trang 13 SGK Toán 11 tập 1 - Chân trời sáng tạo chứa các bài tập vận dụng kiến thức về giới hạn để tính giới hạn của các hàm số đơn giản. Các bài tập này thường yêu cầu học sinh áp dụng các tính chất của giới hạn và các dạng giới hạn cơ bản.
Ví dụ, bài 1 yêu cầu tính limx→2 (x2 + 1). Để giải bài này, ta có thể áp dụng tính chất limx→a (f(x) + g(x)) = limx→a f(x) + limx→a g(x) và limx→a xn = an. Do đó, limx→2 (x2 + 1) = limx→2 x2 + limx→2 1 = 22 + 1 = 5.
Trang 14 SGK Toán 11 tập 1 - Chân trời sáng tạo chứa các bài tập phức tạp hơn, yêu cầu học sinh phải vận dụng linh hoạt các kiến thức đã học và kết hợp với các kỹ năng biến đổi đại số. Các bài tập này thường liên quan đến việc xét giới hạn của các hàm số có chứa căn thức, giá trị tuyệt đối hoặc các biểu thức phức tạp khác.
Ví dụ, bài 3 yêu cầu tính limx→1 (x2 - 1) / (x - 1). Bài này có thể được giải bằng cách phân tích tử thức thành nhân tử: (x2 - 1) = (x - 1)(x + 1). Do đó, limx→1 (x2 - 1) / (x - 1) = limx→1 (x + 1) = 1 + 1 = 2.
Trang 15 SGK Toán 11 tập 1 - Chân trời sáng tạo chứa các bài tập ứng dụng kiến thức về giới hạn để xét tính liên tục của hàm số. Một hàm số được gọi là liên tục tại một điểm nếu giới hạn của hàm số tại điểm đó bằng giá trị của hàm số tại điểm đó.
Ví dụ, bài 5 yêu cầu xét tính liên tục của hàm số f(x) = (x2 - 1) / (x - 1) tại x = 1. Để giải bài này, ta cần tính limx→1 f(x) và so sánh với f(1). Ta đã biết limx→1 f(x) = 2. Tuy nhiên, hàm số f(x) không xác định tại x = 1, do đó hàm số không liên tục tại x = 1.
Hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh đã có thể tự tin giải các bài tập trong mục 1 trang 13, 14, 15 SGK Toán 11 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt!