Giải mục 1 trang 88, 89 SGK Toán 11 tập 1 - Chân trời sáng tạo

Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 88, 89 sách giáo khoa Toán 11 tập 1 chương trình Chân trời sáng tạo.

Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.

Mặt bàn, mặt bảng cho ta hình ảnh một phần của mặt phẳng. Hãy chỉ thêm các ví dụ khác về hình ảnh một phần của mặt phẳng.

Hoạt động 1

Mặt bàn, mặt bảng cho ta hình ảnh một phần của mặt phẳng. Hãy chỉ thêm các ví dụ khác về hình ảnh một phần của mặt phẳng.

Phương pháp giải:

Quan sát hình ảnh thực tế và trả lời câu hỏi.

Lời giải chi tiết:

Một số hình ảnh một phần của mặt phẳng trong thực tế là: sàn nhà, mặt tường,…

Thực hành 1

a) Vẽ hình biểu diễn của một hình hộp chữ nhật.

b) Quan sát Hình 4a và cho biết điểm nào thuộc, điểm nào không thuộc mặt phẳng \(\left( P \right)\).

c) Quan sát Hình 4b và cho biết điểm nào thuộc, điểm nào không thuộc mặt phẳng \(\left( Q \right)\).

Phương pháp giải:

• Vẽ hình biểu diễn của một hình không gian theo quy tắc:

‒ Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.

– Giữ nguyên tính liên thuộc (thuộc hay không thuộc) giữa điểm với đường thẳng hoặc với đoạn thẳng.

‒ Giữ nguyên tính tính song song, tính cắt nhau giữa các đường thẳng.

– Biểu diễn đường nhìn thấy bằng nét vẽ liền và biểu diễn đường bị che khuất bằng nét vẽ đứt đoạn.

• Điểm thuộc, không thuộc mặt phẳng:

‒ Nếu điểm \(A\) thuộc mặt phẳng \(\left( P \right)\) thì ta nói \(A\) nằm trên \(\left( P \right)\) hay \(\left( P \right)\) chứa \(A\), hay \(\left( P \right)\) đi qua \(A\).

– Nếu điểm \(B\) không thuộc mặt phẳng \(\left( P \right)\) thì ta nói \(B\) nằm ngoài \(\left( P \right)\) hay \(\left( P \right)\) không chứa \(B\).

Lời giải chi tiết:

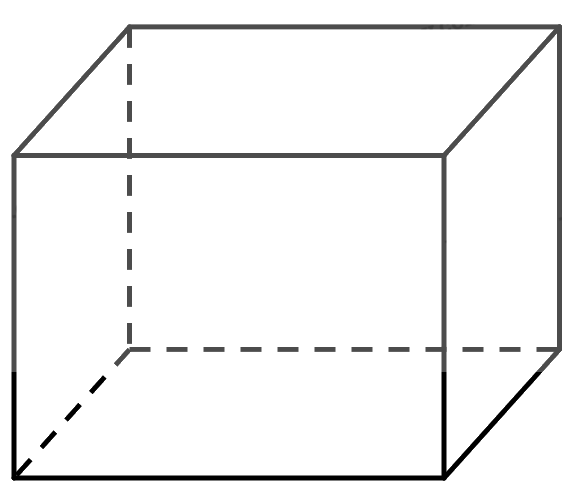
Giải mục 1 trang 88, 89 SGK Toán 11 tập 1 - Chân trời sáng tạo 1

b) Các điểm thuộc mặt phẳng \(\left( P \right)\) là: \(A',B',C',D'\).

Các điểm không thuộc mặt phẳng \(\left( P \right)\) là: \(A,B,C,D\).

c) Các điểm thuộc mặt phẳng \(\left( Q \right)\) là: \(A,C,D\).

Các điểm không thuộc mặt phẳng \(\left( Q \right)\) là: \(B\).

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải mục 1 trang 88, 89 SGK Toán 11 tập 1 - Chân trời sáng tạo – hành trang không thể thiếu trong chuyên mục toán lớp 11 trên nền tảng học toán. Bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải mục 1 trang 88, 89 SGK Toán 11 tập 1 - Chân trời sáng tạo: Tổng quan

Mục 1 của chương trình Toán 11 tập 1 Chân trời sáng tạo tập trung vào việc giới thiệu về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng, mở đầu cho chương trình Giải tích. Việc hiểu rõ về giới hạn sẽ giúp học sinh tiếp cận các khái niệm phức tạp hơn như đạo hàm và tích phân một cách dễ dàng hơn.

Nội dung chính của mục 1 trang 88, 89

Mục 1 bao gồm các nội dung chính sau:

Khái niệm giới hạn của hàm số tại một điểm: Định nghĩa giới hạn, ý nghĩa của giới hạn, cách kiểm tra sự tồn tại của giới hạn.
Giới hạn một bên: Giới hạn bên trái, giới hạn bên phải, điều kiện để giới hạn tồn tại.
Các tính chất của giới hạn: Tổng, hiệu, tích, thương của các giới hạn.
Ví dụ minh họa: Các bài tập cụ thể giúp học sinh hiểu rõ hơn về các khái niệm và tính chất đã học.

Giải chi tiết bài tập mục 1 trang 88, 89

Dưới đây là lời giải chi tiết cho từng bài tập trong mục 1 trang 88, 89 SGK Toán 11 tập 1 Chân trời sáng tạo:

Bài 1: Tính các giới hạn sau

lim (x→2) (x^2 + 3x - 1)
lim (x→-1) (2x^3 - 5x + 2)
lim (x→0) (x + 1)/(x - 1)

Lời giải:

lim (x→2) (x^2 + 3x - 1) = 2^2 + 3*2 - 1 = 4 + 6 - 1 = 9
lim (x→-1) (2x^3 - 5x + 2) = 2*(-1)^3 - 5*(-1) + 2 = -2 + 5 + 2 = 5
lim (x→0) (x + 1)/(x - 1) = (0 + 1)/(0 - 1) = 1/-1 = -1

Bài 2: Tính các giới hạn sau

lim (x→3) (x^2 - 9)/(x - 3)
lim (x→1) (x^3 - 1)/(x - 1)

Lời giải:

lim (x→3) (x^2 - 9)/(x - 3) = lim (x→3) (x - 3)(x + 3)/(x - 3) = lim (x→3) (x + 3) = 3 + 3 = 6
lim (x→1) (x^3 - 1)/(x - 1) = lim (x→1) (x - 1)(x^2 + x + 1)/(x - 1) = lim (x→1) (x^2 + x + 1) = 1^2 + 1 + 1 = 3

Bài 3: Cho hàm số f(x) = x^2 + 1. Tính f(2), f(2.1), f(2.01), f(2.001). So sánh các kết quả với 5.

Lời giải:

f(2) = 2^2 + 1 = 5
f(2.1) = (2.1)^2 + 1 = 4.41 + 1 = 5.41
f(2.01) = (2.01)^2 + 1 = 4.0401 + 1 = 5.0401
f(2.001) = (2.001)^2 + 1 = 4.004001 + 1 = 5.004001

Nhận thấy khi x tiến gần đến 2, f(x) tiến gần đến 5.

Mẹo giải bài tập về giới hạn

Phân tích mẫu thức: Nếu mẫu thức có thể phân tích thành nhân tử, hãy thử rút gọn biểu thức.
Sử dụng các công thức giới hạn: Nắm vững các công thức giới hạn cơ bản để áp dụng vào giải bài tập.
Biến đổi đại số: Sử dụng các phép biến đổi đại số để đưa biểu thức về dạng đơn giản hơn.
Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

Kết luận

Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em học sinh đã hiểu rõ hơn về nội dung mục 1 trang 88, 89 SGK Toán 11 tập 1 Chân trời sáng tạo. Chúc các em học tập tốt!