Chào mừng bạn đến với chuyên mục lý thuyết Phương trình, bất phương trình mũ và lôgarit dành cho học sinh lớp 11 chương trình Chân trời sáng tạo tại giaitoan.edu.vn. Đây là một trong những chủ đề quan trọng của môn Toán, đòi hỏi sự nắm vững kiến thức nền tảng và kỹ năng giải quyết vấn đề.
Chúng tôi cung cấp hệ thống lý thuyết đầy đủ, dễ hiểu, cùng với các ví dụ minh họa chi tiết, giúp bạn tiếp thu kiến thức một cách hiệu quả nhất.
1. Phương trình mũ cơ bản Phương trình mũ cơ bản có dạng \({a^x} = b\)(với \(a > 0,a \ne 1\)).
1. Phương trình mũ cơ bản
Phương trình mũ cơ bản có dạng \({a^x} = b\)(với \(a > 0,a \ne 1\)).
- Nếu b > 0 thì phương trình có nghiệm duy nhất \(x = {\log _a}b\).
- Nếu b \( \le \) 0 thì phương trình vô nghiệm.
Chú ý: Với \(a > 0,a \ne 1\)
a) \({a^x} = {a^\alpha } \Leftrightarrow x = \alpha \).
b) Tổng quát hơn, \({a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) = v\left( x \right)\)
Minh họa bằng đồ thị:
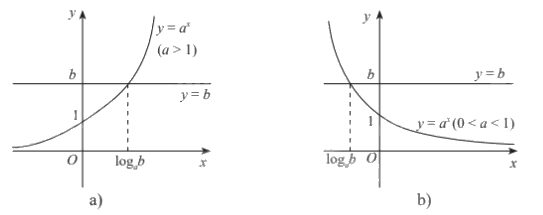
2. Phương trình lôgarit cơ bản
Phương trình lôgarit cơ bản có dạng \({\log _a}x = b\left( {a > 0,a \ne 1} \right)\).
Phương trình luôn có nghiệm duy nhất \(x = {a^b}\).
Chú ý: Với \(a > 0,a \ne 1\)
a) \({\log _a}u\left( x \right) = b \Leftrightarrow u\left( x \right) = {a^b}\).
b) \({\log _a}u\left( x \right) = {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) = v\left( x \right)\end{array} \right.\).
Có thể thay \(u\left( x \right) > 0\) bằng \(v\left( x \right) > 0\) (chọn bất phương trình đơn giản hơn)
Minh họa bằng đồ thị:
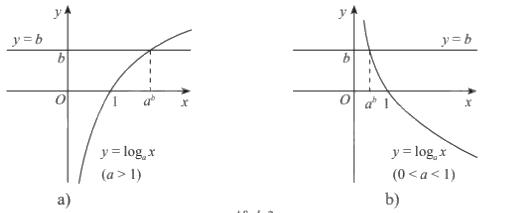
3. Bất phương trình mũ cơ bản
Bất phương trình mũ cơ bản có dạng \({a^x} > b\) (hoặc \({a^x} \ge b,{a^x} < b,{a^x} \le b\)) với \(a > 0,a \ne 1\).
Bảng tổng kết về nghiệm của các bất phương trình trên:

Chú ý:
Nếu a > 1 thì \({a^{u\left( x \right)}} = {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) > v\left( x \right)\).
Nếu 0 < a < 1 thì \({a^{u\left( x \right)}} > {a^{v\left( x \right)}} \Leftrightarrow u\left( x \right) < v\left( x \right)\).
4. Bất phương trình lôgarit cơ bản
Bất phương trình lôgarit cơ bản có dạng \({\log _a}x > b\)(hoặc \({\log _a}x \ge b,{\log _a}x < b,{\log _a}x \le b\)) với \(a > 0,a \ne 1\).
Bảng tổng kết về nghiệm của các bất phương trình trên:

Chú ý:
Nếu a > 1 thì \({\log _a}u\left( x \right) > {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}v\left( x \right) > 0\\u\left( x \right) > v\left( x \right)\end{array} \right.\).
Nếu 0 < a < 1 thì \({\log _a}u\left( x \right) > {\log _a}v\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}u\left( x \right) > 0\\u\left( x \right) < v\left( x \right)\end{array} \right.\).
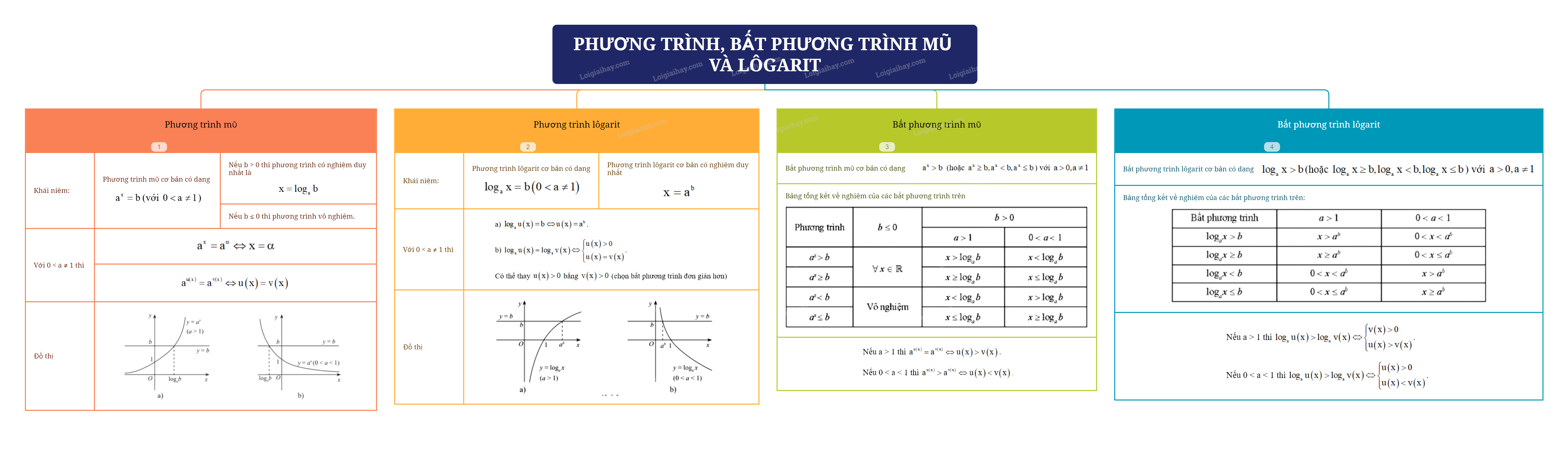
Chương trình Toán 11 Chân trời sáng tạo đi sâu vào các khái niệm về phương trình mũ, bất phương trình mũ, hàm số mũ và hàm số lôgarit. Việc nắm vững lý thuyết là bước đầu tiên quan trọng để giải quyết các bài toán liên quan.
Phương trình mũ là phương trình có chứa ẩn số trong số mũ. Dạng tổng quát của phương trình mũ là: af(x) = b, trong đó a là một số dương khác 1, và f(x) là một biểu thức chứa ẩn số x.
Để giải phương trình mũ, ta thường sử dụng các phương pháp sau:
Bất phương trình mũ là bất phương trình có chứa ẩn số trong số mũ. Dạng tổng quát của bất phương trình mũ là: af(x) > b hoặc af(x) < b, trong đó a là một số dương khác 1, và f(x) là một biểu thức chứa ẩn số x.
Khi giải bất phương trình mũ, cần chú ý đến tính đơn điệu của hàm số mũ:
Dựa vào tính đơn điệu của hàm số mũ, ta có thể so sánh các số mũ để giải bất phương trình.
Hàm số mũ có dạng y = ax, trong đó a > 0 và a ≠ 1. Hàm số lôgarit có dạng y = logax, trong đó a > 0 và a ≠ 1.
Các tính chất quan trọng của hàm số mũ và hàm số lôgarit:
Các bài tập về phương trình, bất phương trình mũ và lôgarit thường gặp các dạng sau:
Để nắm vững kiến thức về phương trình, bất phương trình mũ và lôgarit, bạn cần luyện tập thường xuyên với các bài tập khác nhau. Giaitoan.edu.vn cung cấp một hệ thống bài tập phong phú, đa dạng, được phân loại theo mức độ khó, giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.
Hy vọng rằng, với những kiến thức và hướng dẫn trên, bạn sẽ học tập hiệu quả và đạt kết quả tốt trong môn Toán 11 Chân trời sáng tạo.