Bài 1 trang 81 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc ôn tập chương 3: Cấp số cho và cấp số nhân. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải các bài toán liên quan đến cấp số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp (S.ABCD), đáy (ABCD) là hình thoi cạnh (a) có (O) là giao điểm của hai đường chéo
Đề bài
Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình thoi cạnh \(a\) có \(O\) là giao điểm của hai đường chéo, \(\widehat {ABC} = {60^ \circ },SO \bot \left( {ABCD} \right),SO = a\sqrt 3 \). Tính khoảng cách từ \(O\) đến mặt phẳng \(\left( {SCD} \right)\).
Phương pháp giải - Xem chi tiết
Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng.
Lời giải chi tiết
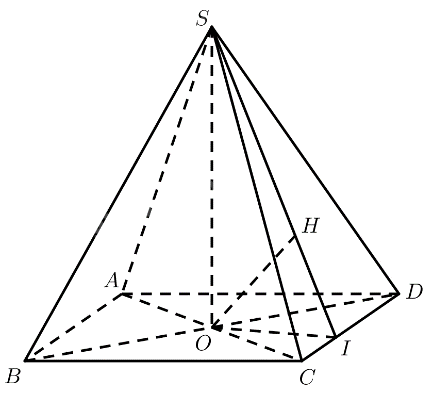
Kẻ \(OI \bot C{\rm{D}}\left( {I \in C{\rm{D}}} \right),OH \bot SI\left( {H \in SI} \right)\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SO \bot \left( {ABCD} \right) \Rightarrow SO \bot C{\rm{D}}\\OI \bot C{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {SOI} \right)\\\left. \begin{array}{l} \Rightarrow C{\rm{D}} \bot OH\\OH \bot SI\end{array} \right\} \Rightarrow OH \bot \left( {SC{\rm{D}}} \right)\\ \Rightarrow d\left( {O,\left( {SC{\rm{D}}} \right)} \right) = OH\end{array}\)
\(\Delta ABC\) đều \( \Rightarrow AC = a \Rightarrow OC = \frac{1}{2}AC = \frac{a}{2}\)
\(\Delta ABD\) có \(\widehat {BA{\rm{D}}} = {120^ \circ } \Rightarrow B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2} - 2{\rm{A}}B.A{\rm{D}}} = a\sqrt 3 \Rightarrow OD = \frac{1}{2}B{\rm{D}} = \frac{{a\sqrt 3 }}{2}\)
\(\Delta OCD\) vuông tại \(O\) có đường cao \(OI\)
\( \Rightarrow OI = \frac{{OC.O{\rm{D}}}}{{C{\rm{D}}}} = \frac{{a\sqrt 3 }}{4}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OI \Rightarrow \Delta SOI\) vuông tại \(O\) có đường cao \(OH\)
\( \Rightarrow OH = \frac{{SO.OI}}{{\sqrt {S{O^2} + O{I^2}} }} = \frac{{a\sqrt {51} }}{{17}}\)
Vậy \(d\left( {O,\left( {SCD} \right)} \right) = OH = \frac{{a\sqrt {51} }}{{17}}\).
Bài 1 trang 81 SGK Toán 11 tập 2 Chân trời sáng tạo là một bài tập quan trọng trong chương trình ôn tập về cấp số cho và cấp số nhân. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Dưới đây là nội dung chi tiết của bài tập và lời giải:
(Nội dung bài tập sẽ được chèn vào đây. Ví dụ: Cho cấp số cho có số hạng đầu u1 = 2 và công sai d = 3. Tìm số hạng thứ 5 của cấp số.)
Để giải bài tập này, chúng ta sẽ sử dụng công thức số hạng tổng quát của cấp số cho: un = u1 + (n - 1)d
Trong đó:
Áp dụng công thức vào bài tập, ta có:
u5 = u1 + (5 - 1)d = 2 + (4)3 = 2 + 12 = 14
Vậy, số hạng thứ 5 của cấp số là 14.
Ngoài bài tập trên, học sinh có thể gặp các dạng bài tập tương tự như:
Để giải các bài tập về cấp số cho và cấp số nhân một cách hiệu quả, học sinh nên:
(Thêm một vài ví dụ minh họa khác để học sinh hiểu rõ hơn về cách giải bài tập.)
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải Bài 1 trang 81 SGK Toán 11 tập 2 – Chân trời sáng tạo và các bài tập tương tự. Chúc các em học tốt!
Lưu ý: Bài giải trên chỉ mang tính chất tham khảo. Học sinh nên tự mình suy nghĩ và giải bài tập để hiểu rõ hơn về kiến thức.