Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 1 trang 52, 53 SGK Toán 11 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập trong mục này tập trung vào các kiến thức cơ bản về phép toán, các khái niệm quan trọng trong chương trình Toán 11.
Tìm điểm giống nhau của các dãy số sau:
Tìm điểm giống nhau của các dãy số sau:
a) 2; 5; 8; 11; 14 (xem Hình 1).
b) 2; 4; 6; 8.
c) 5; 10; 15; 20; 25.
d) ‒5; ‒2; 1; 4; 7; 10.
Phương pháp giải:
Xem hai số hạng liên tiếp của dãy có liên hệ gì.
Lời giải chi tiết:
Ta thấy:
a) Số sau hơn số liền trước 3 đơn vị.
b) Số sau hơn số liền trước 2 đơn vị.
c) Số sau hơn số liền trước 5 đơn vị.
d) Số sau hơn số liền trước 3 đơn vị.
Điểm giống nhau của các dãy số này là hai số hạng liền nhau hơn kém nhau một số không đổi.
Chứng minh mỗi dãy số sau là cấp số cộng. Xác định công sai của mỗi cấp số cộng đó.
a) 3; 7; 11; 15; 19; 23.
b) Dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 9n - 9\).
c) Dãy số \(\left( {{v_n}} \right)\) với \({v_n} = an + b\), trong đó \(a\) và \(b\) là các hằng số.
Phương pháp giải:
Biến đổi, đưa \({u_{n + 1}} = {u_n} + d\), khi đó dãy số là cấp số cộng có công sai \(d\).
Lời giải chi tiết:
a) Dãy số: 3; 7; 11; 15; 19; 23 là cấp số cộng có công sai \(d = 4\).
b) Ta có: \({u_{n + 1}} = 9\left( {n + 1} \right) - 9 = 9n + 9 - 9 = \left( {9n - 9} \right) + 9 = {u_n} + 9\).
Vậy dãy số \(\left( {{u_n}} \right)\) là cấp số cộng có công sai \({\rm{d}} = 9\).
c) Ta có: \({v_{n + 1}} = a\left( {n + 1} \right) + b = an + a + b = \left( {an + b} \right) + a = {v_n} + a\).
Vậy dãy số \(\left( {{v_n}} \right)\) là cấp số cộng có công sai \({\rm{d}} = a\).
Số đo ba góc của một tam giác vuông lập thành cấp số cộng. Tìm số đo ba góc đó.
Phương pháp giải:
Dựa vào tính chất:
‒ Tam giác vuông có một góc bằng \({90^ \circ }\).
‒ Tổng ba góc trong tam giác bằng \({180^ \circ }\).
Lời giải chi tiết:
Do tam giác đó là tam giác vuông nên có một góc bằng \({90^ \circ }\).
Giả sử hai góc còn lại của tam giác có số đo lần lượt là \(a,b\left( {{0^ \circ } < a,b < {{90}^ \circ }} \right)\).
Vì tổng ba góc trong tam giác bằng \({180^ \circ }\) nên ta có: \(a + b + {90^ \circ } = {180^ \circ } \Leftrightarrow a + b = {90^ \circ }\)(1).
Vì số đo ba góc trong tam giác lập thành cấp số cộng nên ta có:
\(b = \frac{{a + {{90}^ \circ }}}{2} \Leftrightarrow 2b = a + {90^ \circ } \Leftrightarrow - a + 2b = {90^ \circ }\) (2)
Từ (1) và (2) ta có hệ phương trình sau:
\(\left\{ \begin{array}{l}a + b = {90^ \circ }\\ - a + 2b = {90^ \circ }\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = {30^ \circ }\\b = {60^ \circ }\end{array} \right.\)
Vậy số đo ba góc của tam giác vuông đó lần lượt là: \({30^ \circ };{60^ \circ };{90^ \circ }\).
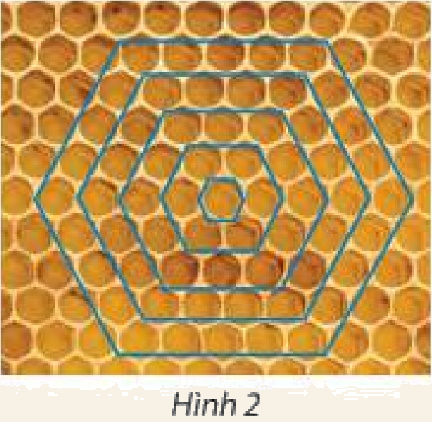
Mặt cắt của một tổ ong có hình lưới tạo bởi các ô hình lục giác đều. Từ một ô đầu tiên, bước thứ nhất, các ong thợ tạo ra vòng 1 gồm 6 ô lục giác; bước thứ hai, các ong thợ sẽ tạo ra vòng 2 có 12 ô bao quanh vòng 1; bước thứ ba, các ong thợ sẽ tạo ra 18 ô bao quanh vòng 2; cứ thế tiếp tục (Hình 2). Số ô trên các vòng theo thứ tự có tạo thành cấp số cộng không? Nếu có, tìm công sai của cấp số cộng này.

Phương pháp giải:
Biến đổi, đưa \({u_{n + 1}} = {u_n} + d\), khi đó dãy số là cấp số cộng có công sai \(d\).
Lời giải chi tiết:
Ta có: Dãy số chỉ số ô trên các vòng là: \({u_1} = 6;{u_2} = 12;{u_3} = 18;...\)
Ta thấy: \({u_{n + 1}} = {u_n} + 6\)
Vậy ô trên các vòng theo thứ tự tạo thành cấp số cộng có công sai \({\rm{d}} = 6\).
Mục 1 trang 52, 53 SGK Toán 11 tập 1 Chân trời sáng tạo là phần khởi đầu quan trọng của chương trình học, tập trung vào việc ôn tập và củng cố kiến thức về phép toán, đặc biệt là các phép toán trên tập số thực. Việc nắm vững kiến thức này là nền tảng để học tốt các phần tiếp theo của chương trình.
Bài tập này yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia trên tập số thực. Để giải bài tập này, học sinh cần nắm vững các quy tắc về thứ tự thực hiện các phép toán và các tính chất của các phép toán.
Ví dụ:
| Bài tập | Lời giải |
|---|---|
| a) 2 + 3 x 4 | 2 + 3 x 4 = 2 + 12 = 14 |
| b) (5 - 2) x 3 | (5 - 2) x 3 = 3 x 3 = 9 |
Bài tập này yêu cầu học sinh giải các phương trình bậc nhất một ẩn. Để giải bài tập này, học sinh cần nắm vững các quy tắc về chuyển vế và các phép toán trên phương trình.
Ví dụ:
2x + 3 = 7
2x = 7 - 3
2x = 4
x = 2
Bài tập này yêu cầu học sinh tính giá trị của các biểu thức chứa các biến. Để giải bài tập này, học sinh cần thay các giá trị của các biến vào biểu thức và thực hiện các phép tính.
Để học tốt môn Toán, các em cần:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập hiệu quả này, các em sẽ học tốt môn Toán 11 và đạt kết quả cao trong các kỳ thi.