Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 3 trang 16, 17 SGK Toán 11 tập 2 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bài tập mục 3 tập trung vào các kiến thức quan trọng về...
Cho các số thực dương (a,M,N) với (a ne 1). Bạn Quân đã vẽ sơ đồ và tìm ra công thức biến đổi biểu thức ({log _a}left( {MN} right)) như sau:
Cho các số thực dương \(a,M,N\) với \(a \ne 1\). Bạn Quân đã vẽ sơ đồ và tìm ra công thức biến đổi biểu thức \({\log _a}\left( {MN} \right)\) như sau:
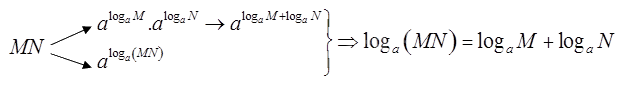
a) Giải thích cách làm của bạn Quân.
b) Vẽ sơ đồ tương tự để tìm công thức biến đổi cho \({\log _a}\frac{M}{N}\) và \({\log _a}{M^\alpha }\left( {\alpha \in \mathbb{R}} \right)\).
Phương pháp giải:
Sử dụng định nghĩa của lôgarit.
Lời giải chi tiết:
a) Ta có: \(M = {a^{{{\log }_a}M}},N = {a^{{{\log }_a}N}} \Rightarrow MN = {a^{{{\log }_a}M}}.{a^{{{\log }_a}N}} = {a^{{{\log }_a}M + {{\log }_a}N}}\)
Mặt khác: \(MN = {a^{{{\log }_a}\left( {MN} \right)}}\)
Vậy \({a^{{{\log }_a}M + {{\log }_a}N}} = {a^{{{\log }_a}\left( {MN} \right)}} \Leftrightarrow {\log _a}M + {\log _a}N = {\log _a}\left( {MN} \right)\)
b)
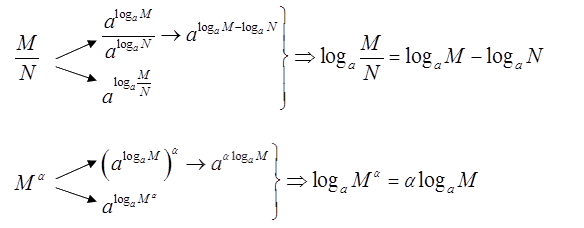
Tính:
a) \({\log _5}4 + {\log _5}\frac{1}{4}\);
b) \({\log _2}28 - {\log _2}7\); c) \(\log \sqrt {1000} \).
Phương pháp giải:
Sử dụng các tính chất của phép tính lôgarit.
Lời giải chi tiết:
a) \({\log _5}4 + {\log _5}\frac{1}{4} = {\log _5}\left( {4.\frac{1}{4}} \right) = {\log _5}1 = 0\).
b) \({\log _2}28 - {\log _2}7 = {\log _2}\frac{{28}}{7} = {\log _2}4 = {\log _2}{2^2} = 2\).
c) \(\log \sqrt {1000} = \log {1000^{\frac{1}{2}}} = \log {\left( {{{10}^3}} \right)^{\frac{1}{2}}} = \log {10^{\frac{3}{2}}} = \frac{3}{2}\).
Độ lớn \(M\) của một trận động đất theo thang Richter được tính theo công thức \(M = \log \frac{A}{{{A_0}}}\), trong đó \(A\) là biên độ lớn nhất ghi được bởi máy đo địa chấn, \({A_0}\) là biên độ tiêu chuẩn được sử dụng để hiệu chỉnh độ lệch gây ra bởi khoảng cách của máy đo địa chấn so với tâm chấn (ở Hoạt động mở đầu và Hoạt động 1, \({A_0} = 1\mu m\)).
a) Tính độ lớn của trận động đất có biên độ \(A\) bằng
i) \({10^{5,1}}{A_0}\); ii) \(65000{A_0}\).
b) Một trận động đất tại địa điểm \(N\) có biên độ lớn nhất gấp ba lần biên độ lớn nhất của trận động đất tại địa điểm \(P\). So sánh độ lớn của hai trận động đất.
Phương pháp giải:
Thay vào công thức tính độ lớn \(M\) và sử dụng tính chất của lôgarit.
Lời giải chi tiết:
a) Với \(A = {10^{5,1}}{A_0}\), ta có: \(M = \log \frac{A}{{{A_0}}} = \log \frac{{{{10}^{5,1}}{A_0}}}{{{A_0}}} = \log {10^{5,1}} = 5,1\) (Richter).
Với \(A = 65000{A_0}\), ta có: \(M = \log \frac{A}{{{A_0}}} = \log \frac{{65000{A_0}}}{{{A_0}}} = \log 65000 \approx 4,81\) (Richter).
b) Với \({A_N} = 3{A_P}\), ta có: \({M_N} = \log \frac{{{A_N}}}{{{A_0}}},{M_P} = \log \frac{{{A_P}}}{{{A_0}}}\).
\({M_N} - {M_P} = \log \frac{{{A_N}}}{{{A_0}}} - \log \frac{{{A_P}}}{{{A_0}}} = \log \left( {\frac{{{A_N}}}{{{A_0}}}:\frac{{{A_P}}}{{{A_0}}}} \right) = \log \frac{{{A_N}}}{{{A_P}}} = \log \frac{{3{A_N}}}{{{A_P}}} = \log 3 \approx 0,48\)
Vậy trận động đất tại địa điểm \(N\) lớn hơn trận động đất tại địa điểm \(P\) 0,48 Richter.
Mục 3 trong SGK Toán 11 tập 2 chương trình Chân trời sáng tạo thường xoay quanh các chủ đề về đạo hàm của hàm số, ứng dụng của đạo hàm trong việc khảo sát hàm số và giải các bài toán thực tế. Việc nắm vững kiến thức và kỹ năng giải các bài tập trong mục này là vô cùng quan trọng để các em có thể đạt kết quả tốt trong các kỳ thi sắp tới.
Lời giải:
Lời giải:
Áp dụng quy tắc tích: y' = (2x) * sin(x) + (x^2 + 1) * cos(x) = 2xsin(x) + (x^2 + 1)cos(x)
Lời giải:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | 0 | - | + |
| y | ↗ | 2 | -2 | ↗ |
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em sẽ tự tin hơn trong việc giải các bài tập mục 3 trang 16, 17 SGK Toán 11 tập 2 chương trình Chân trời sáng tạo. Chúc các em học tập tốt!