Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 3 trang 73, 74, 75 SGK Toán 11 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em hiểu rõ kiến thức, nắm vững phương pháp giải và tự tin làm bài tập.
Giá cước vận chuyển bưu kiện giữa hai thành phố do một đơn vị cung cấp được cho bởi bảng sau:
Giá cước vận chuyển bưu kiện giữa hai thành phố do một đơn vị cung cấp được cho bởi bảng sau:

Nếu chỉ xét trên khoảng từ 0 đến 5 (tính theo 100 gam) thì hàm số giả cước (tính theo nghìn đồng) xác định như sau:
\(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}6&{khi\,\,x \in \left( {0;1} \right]}\\7&{khi\,\,x \in \left( {1;2,5} \right]}\\{10}&{khi\,\,x \in \left( {2,5;5} \right]}\end{array}} \right.\)
Đồ thị của hàm số như Hình 2.
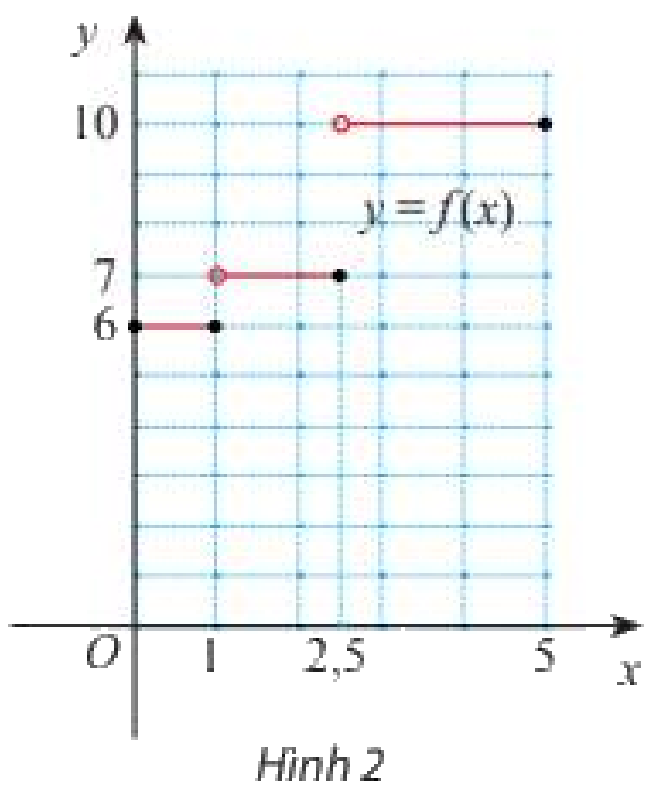
a) Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì sao cho \(x \in \left( {1;2,5} \right)\) và \(\lim {x_n} = 1\). Tìm \(\lim f\left( {{x_n}} \right)\).
b) Giả sử \(\left( {{x_n}'} \right)\) là dãy số bất kì sao cho \({x_n}' \in \left( {0;1} \right)\) và \(\lim {x_n}' = 1\). Tìm \(\lim f\left( {{x_n}'} \right)\).
c) Nhận xét về kết quả ở a) và b)
Phương pháp giải:
Áp dụng công thức tính giới hạn của hằng số.
Lời giải chi tiết:
a) Khi \(x \in \left( {1;2,5} \right)\) thì \(f\left( {{x_n}} \right) = 7\) nên \(\lim f\left( {{x_n}} \right) = \lim 7 = 7\).
b) Khi \({x_n}' \in \left( {0;1} \right)\) thì \(f\left( {{x_n}'} \right) = 6\) nên \(\lim f\left( {{x_n}'} \right) = \lim 6 = 6\).
c) Ta thấy \(\lim {x_n} = \lim {x_n}' = 1\) nhưng \(\lim f\left( {{x_n}} \right) \ne \lim f\left( {{x_n}'} \right)\)
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{1 - 2x}&{khi\,\,x \le - 1}\\{{x^2} + 2}&{khi\,\,x > - 1}\end{array}} \right.\).
Tìm các giới hạn \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to - {1^ - }} {\rm{ }}f\left( x \right)\) và \(\mathop {\lim }\limits_{x \to - 1} f\left( x \right)\) (nếu có).
Phương pháp giải:
− Để tính giới hạn \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to - {1^ - }} {\rm{ }}f\left( x \right)\), ta áp dụng định lý về giới hạn bên trái và giới hạn bên phải của hàm số.
− Để tính giới hạn \(\mathop {\lim }\limits_{x \to - 1} f\left( x \right)\), ta so sánh hai giới hạn \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to - {1^ - }} {\rm{ }}f\left( x \right)\).
• Nếu \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {1^ - }} {\rm{ }}f\left( x \right) = L\) thì \(\mathop {\lim }\limits_{x \to - 1} f\left( x \right) = L\).
• Nếu \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to - {1^ - }} {\rm{ }}f\left( x \right)\) thì không tồn tại \(\mathop {\lim }\limits_{x \to - 1} f\left( x \right)\).
Lời giải chi tiết:
a) Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì, \({x_n} > - 1\) và \({x_n} \to - 1\). Khi đó \(f\left( {{x_n}} \right) = x_n^2 + 2\)
Ta có: \(\lim f\left( {{x_n}} \right) = \lim \left( {x_n^2 + 2} \right) = \lim x_n^2 + \lim 2 = {\left( { - 1} \right)^2} + 2 = 3\)
Vậy \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = 3\).
Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì, \({x_n} < - 1\) và \({x_n} \to - 1\). Khi đó \(f\left( {{x_n}} \right) = 1 - 2{x_n}\).
Ta có: \(\lim f\left( {{x_n}} \right) = \lim \left( {1 - 2{x_n}} \right) = \lim 1 - \lim \left( {2{x_n}} \right) = \lim 1 - 2\lim {x_n} = 1 - 2.\left( { - 1} \right) = 3\)
Vậy \(\mathop {\lim }\limits_{x \to - {1^ - }} f\left( x \right) = 3\).
b) Vì \(\mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {1^ - }} {\rm{ }}f\left( x \right) = 3\) nên \(\mathop {\lim }\limits_{x \to - 1} f\left( x \right) = 3\).
Mục 3 trong SGK Toán 11 tập 1 - Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững lý thuyết, hiểu rõ các định nghĩa, định lý và công thức liên quan. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập, kèm theo các phân tích và giải thích rõ ràng, giúp học sinh hiểu sâu sắc hơn về kiến thức.
Trang 73 thường chứa các bài tập vận dụng kiến thức cơ bản để kiểm tra mức độ hiểu bài của học sinh. Các bài tập này thường yêu cầu học sinh thực hiện các phép tính đơn giản, chứng minh các đẳng thức hoặc giải các phương trình, bất phương trình cơ bản.
Trang 74 thường chứa các bài tập nâng cao hơn, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề phức tạp hơn. Các bài tập này thường yêu cầu học sinh phân tích, tổng hợp, suy luận và đưa ra các kết luận hợp lý.
Trang 75 thường chứa các bài tập tổng hợp, yêu cầu học sinh vận dụng kiến thức từ nhiều chủ đề khác nhau để giải quyết một vấn đề lớn. Các bài tập này thường yêu cầu học sinh có khả năng tư duy sáng tạo, giải quyết vấn đề và làm việc nhóm.
Giải bài tập là một phần quan trọng trong quá trình học tập môn Toán. Việc giải bài tập giúp học sinh củng cố kiến thức, rèn luyện kỹ năng và phát triển tư duy. Đồng thời, việc giải bài tập còn giúp học sinh tự tin hơn khi làm bài kiểm tra và thi cử.
Hy vọng rằng bài viết này đã cung cấp cho các em học sinh những lời giải chi tiết và hữu ích cho các bài tập trong mục 3 trang 73, 74, 75 SGK Toán 11 tập 1 - Chân trời sáng tạo. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!