Chào mừng các em học sinh đến với lời giải chi tiết Bài 6 trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo. Bài học này thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức đã học để giải quyết các bài toán thực tế.
giaitoan.edu.vn cung cấp lời giải bài tập Toán 11 chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Một thấu kính hội tụ có tiêu cự là \(f > 0\) không đổi. Gọi \(d\) và \(d'\) lần lượt là khoảng cách từ vật thật và ảnh của nó tới quang tâm \(O\) của thấu kính (Hình 5). Ta có công thức:
Đề bài
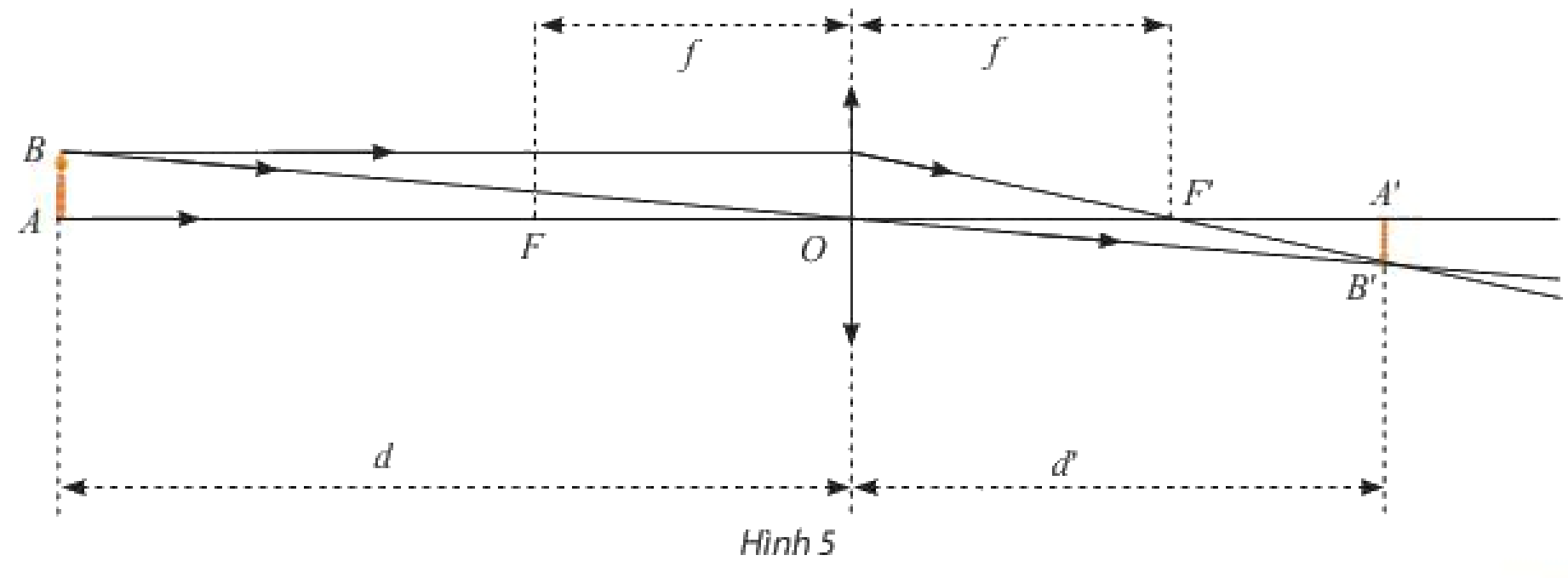
Một thấu kính hội tụ có tiêu cự là \(f > 0\) không đổi. Gọi \(d\) và \(d'\) lần lượt là khoảng cách từ vật thật và ảnh của nó tới quang tâm \(O\) của thấu kính (Hình 5). Ta có công thức: \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\) hay \(d' = \frac{{df}}{{d - f}}\).
Xét hàm số \(g\left( d \right) = \frac{{df}}{{d - f}}\). Tìm các giới hạn sau đây và giải thích ý nghĩa.
a) \(\mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right)\);
b) \(\mathop {\lim }\limits_{d \to + \infty } g\left( d \right)\).
Phương pháp giải - Xem chi tiết
a) Bước 1: Đưa hàm số \(f\left( x \right)\) về tích của hai hàm số, trong đó một hàm số có giới hạn hữu hạn, còn một hàm số có giới hạn vô cực.
Bước 2: Áp dụng quy tắc xét dấu để tính giới hạn của tích.
b) Bước 1: Chia cả tử và mẫu cho lũy thừa bậc cao nhất của tử và mẫu.
Bước 2: Tính các giới hạn của tử và mẫu rồi áp dụng các quy tắc tính giới hạn để tính giới hạn.
Lời giải chi tiết
a) \(\mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} = \mathop {\lim }\limits_{d \to {f^ + }} \left( {df} \right).\mathop {\lim }\limits_{d \to {f^ + }} \frac{1}{{d - f}}\)
Ta có: \(\mathop {\lim }\limits_{d \to {f^ + }} \left( {df} \right) = f\mathop {\lim }\limits_{d \to {f^ + }} d = {f^2};\mathop {\lim }\limits_{d \to {f^ + }} \frac{1}{{d - f}} = + \infty \)
\( \Rightarrow \mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} = + \infty \)
Ý nghĩa: Khi vật dần đến tiêu điểm từ phía xa thấu kính đến gần thấu kính thì khoảng cách từ ảnh đến thấu kính dần đến \( + \infty \).
b) \(\mathop {\lim }\limits_{d \to + \infty } g\left( d \right) = \mathop {\lim }\limits_{d \to + \infty } \frac{{df}}{{d - f}} = \mathop {\lim }\limits_{d \to + \infty } \frac{{df}}{{d\left( {1 - \frac{f}{d}} \right)}} = \mathop {\lim }\limits_{d \to + \infty } \frac{f}{{1 - \frac{f}{d}}} = \frac{f}{{1 - 0}} = f\)
Ý nghĩa: Khi khoảng cách từ vật đến thấu kính càng xa thì ảnh tiến dần đến tiêu điểm của ảnh \(\left( {F'} \right)\).
Bài 6 trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Trước khi đi vào giải bài tập, chúng ta cần ôn lại một số kiến thức lý thuyết quan trọng:
Để giải Bài 6 trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo, chúng ta cần phân tích đề bài, xác định các yếu tố đã cho và yêu cầu của bài toán. Sau đó, áp dụng các kiến thức lý thuyết và các phép toán vectơ để tìm ra lời giải.
(Giả sử đề bài Bài 6 trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo là: Cho tam giác ABC. Gọi M là trung điểm của BC. Tìm vectơ AM theo vectơ AB và AC.)
Lời giải:
Để rèn luyện kỹ năng giải các bài tập về vectơ, các em có thể tham khảo các bài tập tương tự sau:
Khi giải các bài tập về vectơ, các em cần lưu ý một số điểm sau:
Vectơ không chỉ là một khái niệm trừu tượng trong toán học mà còn có nhiều ứng dụng trong thực tế, như:
Hy vọng với lời giải chi tiết và hướng dẫn giải Bài 6 trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo, các em học sinh sẽ hiểu rõ hơn về kiến thức vectơ và tự tin hơn trong quá trình học tập. Chúc các em học tốt!