Bài 4 trang 135 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải nắm vững các công thức đạo hàm cơ bản và kỹ năng giải toán.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 4 trang 135, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Kết quả đo chiều cao của 200 cây keo 3 năm tuổi ở một nông trường được biểu diễn ở biểu đồ dưới đây.
Đề bài
Kết quả đo chiều cao của 200 cây keo 3 năm tuổi ở một nông trường được biểu diễn ở biểu đồ dưới đây.
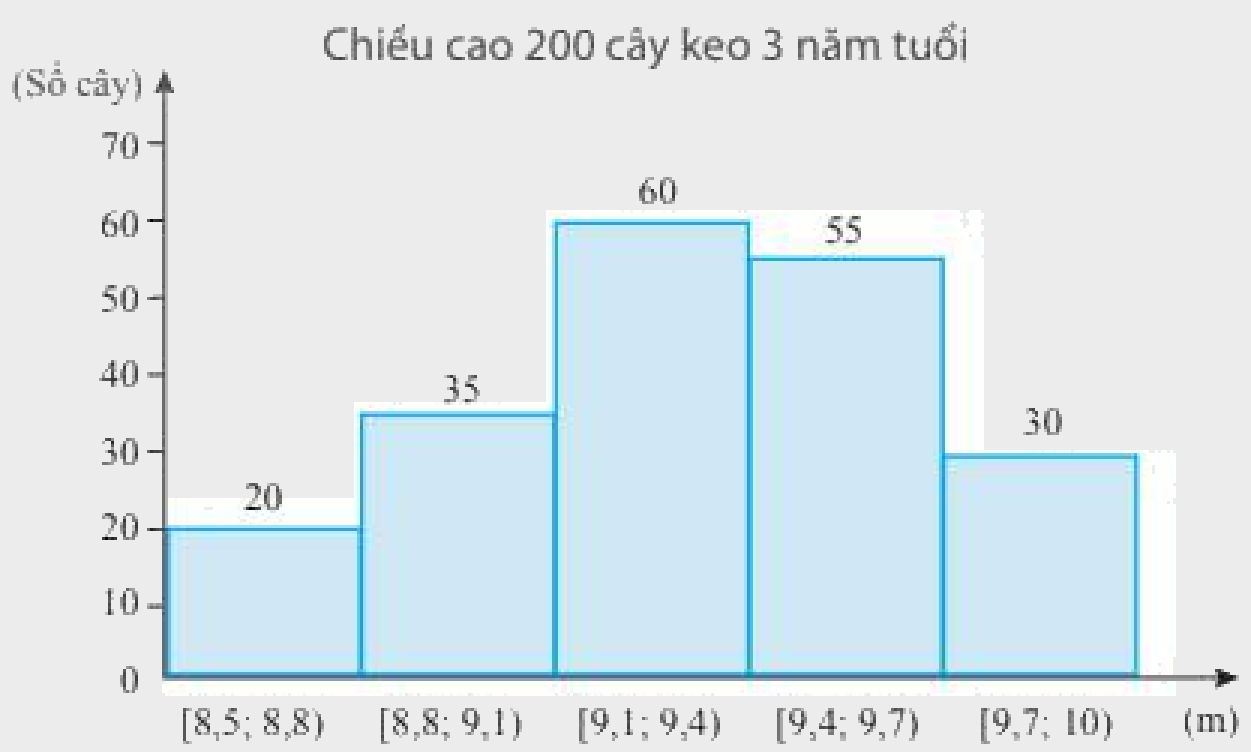
Hãy ước lượng số trung bình và mốt của mẫu số liệu ghép nhóm trên.
Phương pháp giải - Xem chi tiết
Lập bảng tần số ghép lớp sau đó sử dụng các công thức:
‒ Công thức tính trung bình cộng của mẫu số liệu ghép nhóm.
‒ Công thức tính Mốt của mẫu số liệu ghép nhóm.
Lời giải chi tiết
Chiều cao của 200 cây keo 3 năm tuổi được thống kê trong bảng sau:
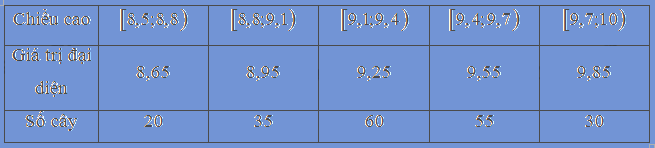
Chiều cao của 200 cây keo 3 năm tuổi sau khi ghép nhóm là:
\(\bar x = \frac{{20.8,65 + 35.8,95 + 60.9,25 + 55.9,55 + 30.9,85}}{{200}} = 9,31\left( m \right)\)
Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\begin{array}{*{20}{c}}{\left[ {9,1;9,4} \right)}\end{array}\).
Do đó: \({u_m} = 9,1;{n_{m - 1}} = 35;{n_m} = 60;{n_{m + 1}} = 55;{u_{m + 1}} - {u_m} = 9,4 - 9,1 = 0,3\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 9,1 + \frac{{60 - 35}}{{\left( {60 - 35} \right) + \left( {60 - 55} \right)}}.0,3 = 9,35\)
Vậy chiều cao của 200 cây keo 3 năm tuổi nhiều nhất là 9,35 mét.
Bài 4 trang 135 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó trong việc giải quyết các bài toán thực tế. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 4 yêu cầu học sinh sử dụng kiến thức về đạo hàm để tìm đạo hàm của các hàm số và giải các bài toán liên quan đến đạo hàm. Cụ thể, bài tập có thể bao gồm các dạng sau:
Để giải Bài 4 trang 135 SGK Toán 11 tập 1 - Chân trời sáng tạo, học sinh cần thực hiện các bước sau:
Ví dụ, xét hàm số f(x) = x2 + 2x + 1. Để tìm đạo hàm của hàm số này, ta sử dụng công thức đạo hàm của hàm số đa thức:
f'(x) = 2x + 2
Đối với các bài tập tính đạo hàm của hàm số lượng giác, học sinh cần nhớ các công thức đạo hàm của các hàm số lượng giác cơ bản, chẳng hạn như:
Đối với các bài tập giải phương trình đạo hàm, học sinh cần sử dụng các kỹ năng giải phương trình đại số để tìm nghiệm của phương trình.
Khi giải Bài 4 trang 135 SGK Toán 11 tập 1 - Chân trời sáng tạo, học sinh cần lưu ý các điểm sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Để củng cố kiến thức về đạo hàm, học sinh có thể giải thêm các bài tập tương tự trong SGK Toán 11 tập 1 - Chân trời sáng tạo hoặc các tài liệu tham khảo khác.
Bài 4 trang 135 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên, các em học sinh sẽ hiểu rõ hơn về bài toán và tự tin giải các bài tập tương tự.