Chào mừng bạn đến với bài học về Lý thuyết Khoảng cách trong không gian, một phần quan trọng của chương trình Toán 11 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức nền tảng và các công thức cần thiết để giải quyết các bài toán liên quan đến khoảng cách trong không gian.
Chúng ta sẽ cùng nhau khám phá cách tính khoảng cách giữa hai điểm, từ một điểm đến một đường thẳng và từ một điểm đến một mặt phẳng trong không gian ba chiều.
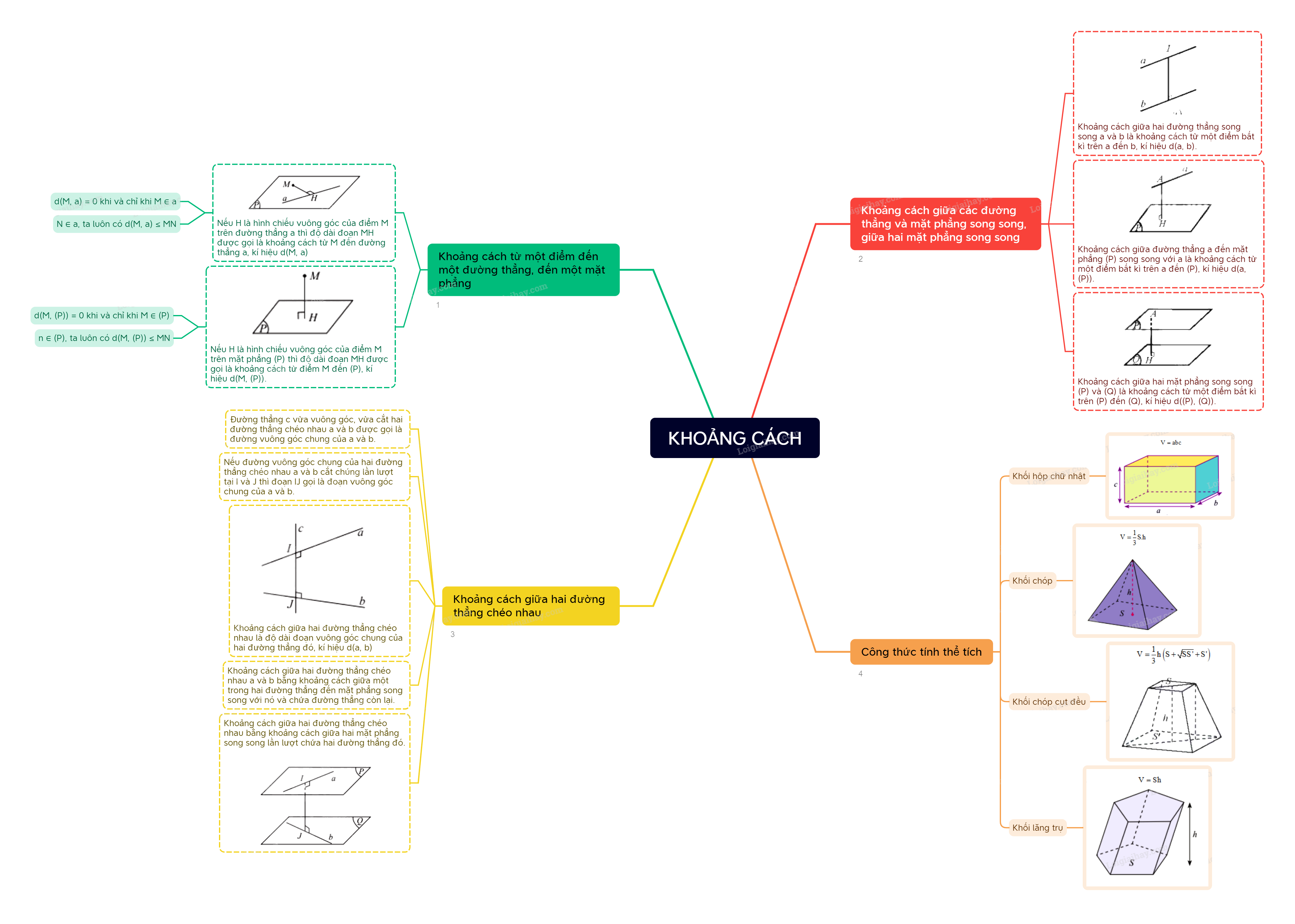
1. Khoảng cách từ một điểm đến một đường thẳng, đến một mặt phẳng
1. Khoảng cách từ một điểm đến một đường thẳng, đến một mặt phẳng
Nếu H là hình chiếu vuông góc của điểm M trên đường thẳng a thì độ dài đoạn MH được gọi là khoảng cách từ M đến đường thẳng a, kí hiệu d(M, a).
Nếu H là hình chiếu vuông góc của điểm M trên mặt phẳng (P) thì độ dài đoạn MH được gọi là khoảng cách từ điểm M đến (P), kí hiệu d(M, (P)).
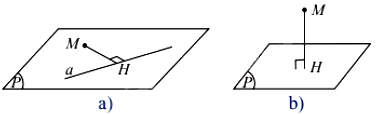
Quy ước:
Nhận xét:
a) Lấy điểm N tùy ý trên đường thẳng a, ta luôn có \(d\left( {M,a} \right) \le MN\).
b) Lấy điểm N tùy ý trên mặt phẳng \(\left( P \right)\), ta luôn có \(d\left( {M,\left( P \right)} \right) \le MN\).
2. Khoảng cách giữa các đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song
Khoảng cách giữa hai đường thẳng song song a và b là khoảng cách từ một điểm bất kì trên a đến b, kí hiệu d(a, b).
Khoảng cách giữa đường thẳng a đến mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì trên a đến (P), kí hiệu d(a, (P)).
Khoảng cách giữa hai mặt phẳng song song (P) và (Q) là khoảng cách từ một điểm bất kì trên (P) đến (Q), kí hiệu d((P), (Q)).
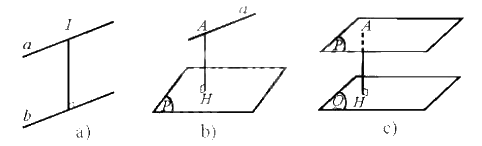
3. Khoảng cách giữa hai đường thẳng chéo nhau
Đường thẳng c vừa vuông góc, vừa cắt hai đường thẳng chéo nhau a và b được gọi là đường vuông góc chung của a và b.
Nếu đường vuông góc chung của hai đường thẳng chéo nhau a và b cắt chúng lần lượt tại I và J thì đoạn IJ gọi là đoạn vuông góc chung của a và b.
Khoảng cách giữa hai đường thẳng chéo nhau là độ dài đoạn vuông góc chung của hai đường thẳng đó, kí hiệu d(a, b)
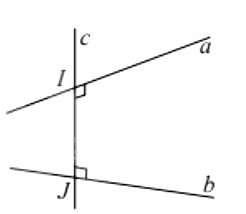
Chú ý:
a) Khoảng cách giữa hai đường thẳng chéo nhau a và b bằng khoảng cách giữa một trong hai đường thẳng đến mặt phẳng song song với nó và chứa đường thẳng còn lại.
b) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó.
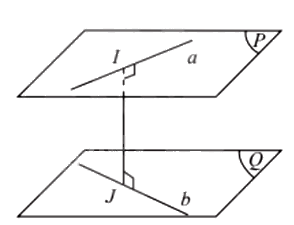
4. Công thức tính thể tích của khối chóp, khối lăng trụ, khối hộp
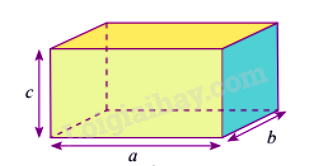
Thể tích khối hộp chữ nhật bằng ba kích thước:
\(V = abc\)
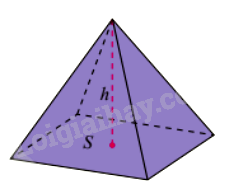
Thể tích khối chóp bằng một phần ba diện tích đáy nhân với chiều cao:
\(V = \frac{1}{3}S.h\)
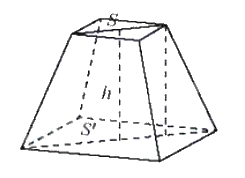
Thể tích khối chóp cụt đều có chiều cao h và diện tích hai đáy S, S’:
\(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right)\)
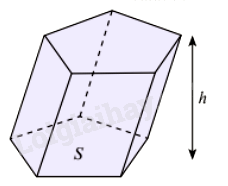
Thể tích khối lăng trụ bằng tích diện tích đáy và chiều cao:
\(V = Sh\)
Trong chương trình Toán 11 Chân trời sáng tạo, phần Hình học không gian đóng vai trò quan trọng, và việc nắm vững lý thuyết về khoảng cách là nền tảng để giải quyết các bài toán phức tạp hơn. Bài viết này sẽ trình bày chi tiết lý thuyết về khoảng cách trong không gian, bao gồm các định nghĩa, công thức và ví dụ minh họa.
Trong không gian Oxyz, cho hai điểm A(xA, yA, zA) và B(xB, yB, zB). Khoảng cách giữa hai điểm A và B được tính theo công thức:
AB = √((xB - xA)2 + (yB - yA)2 + (zB - zA)2)
Ví dụ: Cho A(1, 2, 3) và B(4, 5, 6). Khi đó:
AB = √((4-1)2 + (5-2)2 + (6-3)2) = √(32 + 32 + 32) = √27 = 3√3
Cho điểm M(x0, y0, z0) và đường thẳng Δ có phương trình:
{ x = x0 + at y = y0 + bt z = z0 + ct }
Khoảng cách d từ điểm M đến đường thẳng Δ được tính theo công thức:
d = |[ (x0 - x1)b - (y0 - y1)a ] / √(a2 + b2 + c2)|
Trong đó (x1, y1, z1) là một điểm thuộc đường thẳng Δ.
Cho điểm M(x0, y0, z0) và mặt phẳng (P) có phương trình:
Ax + By + Cz + D = 0
Khoảng cách d từ điểm M đến mặt phẳng (P) được tính theo công thức:
d = |Ax0 + By0 + Cz0 + D| / √(A2 + B2 + C2)
Ví dụ: Cho điểm M(1, 2, 3) và mặt phẳng (P): 2x - y + z + 1 = 0. Khi đó:
d = |2(1) - 2 + 3 + 1| / √(22 + (-1)2 + 12) = |4| / √6 = 4/√6 = (4√6)/6 = (2√6)/3
Lý thuyết khoảng cách trong không gian có nhiều ứng dụng trong thực tế, chẳng hạn như:
Để củng cố kiến thức về lý thuyết khoảng cách trong không gian, bạn có thể thực hành giải các bài tập sau:
Lý thuyết Khoảng cách trong không gian là một phần quan trọng của chương trình Toán 11 Chân trời sáng tạo. Việc nắm vững lý thuyết này sẽ giúp bạn giải quyết các bài toán hình học không gian một cách hiệu quả và chính xác. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích và giúp bạn tự tin hơn trong việc học tập.