Bài 2 trang 126 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến đạo hàm. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tìm đạo hàm của hàm số và giải các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 2 trang 126, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
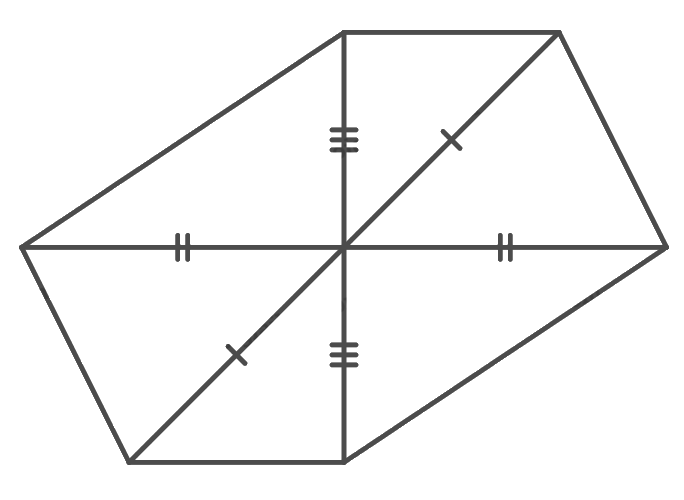
Vẽ hình biểu diễn của một lục giác đều
Đề bài
Vẽ hình biểu diễn của một lục giác đều.
Phương pháp giải - Xem chi tiết
Sử dụng các quy tắc vẽ hình biểu diễn và tính chất của lục giác đều.
Lời giải chi tiết
Lục giác đều có các cặp cạnh đối bằng nhau và song song với nhau, các đường chéo của 2 đỉnh đối diện cắt nhau tại trung điểm mỗi đường. Vậy ta có hình biểu diễn như sau:
Bài 2 trang 126 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm và công thức liên quan đến đạo hàm của hàm số.
Bài 2 yêu cầu học sinh tìm đạo hàm của các hàm số sau:
Để tìm đạo hàm của f(x), ta sử dụng quy tắc đạo hàm của tổng và tích của các hàm số. Cụ thể:
f'(x) = d/dx (3x^2) - d/dx (5x) + d/dx (2)
Áp dụng quy tắc đạo hàm của lũy thừa, ta có:
d/dx (3x^2) = 3 * 2x = 6x
d/dx (5x) = 5
d/dx (2) = 0
Vậy, f'(x) = 6x - 5
Tương tự như câu a, ta tìm đạo hàm của g(x) như sau:
g'(x) = d/dx (x^3) + d/dx (4x) - d/dx (1)
Áp dụng quy tắc đạo hàm của lũy thừa, ta có:
d/dx (x^3) = 3x^2
d/dx (4x) = 4
d/dx (1) = 0
Vậy, g'(x) = 3x^2 + 4
Để tìm đạo hàm của h(x), ta sử dụng quy tắc đạo hàm của tích hai hàm số:
h'(x) = d/dx (x^2 + 1) * (x - 2) + (x^2 + 1) * d/dx (x - 2)
Ta có:
d/dx (x^2 + 1) = 2x
d/dx (x - 2) = 1
Vậy, h'(x) = 2x(x - 2) + (x^2 + 1) * 1 = 2x^2 - 4x + x^2 + 1 = 3x^2 - 4x + 1
Thông qua việc giải Bài 2 trang 126 SGK Toán 11 tập 1 - Chân trời sáng tạo, học sinh đã được rèn luyện kỹ năng tìm đạo hàm của các hàm số đơn giản và phức tạp. Việc nắm vững các quy tắc đạo hàm là rất quan trọng để giải các bài toán liên quan đến đạo hàm trong chương trình học.
Để củng cố kiến thức về đạo hàm, học sinh có thể tham khảo các bài tập tương tự trong SGK Toán 11 tập 1 - Chân trời sáng tạo và các tài liệu luyện tập khác. Ngoài ra, học sinh cũng có thể tìm kiếm các bài giảng trực tuyến và video hướng dẫn giải bài tập để hiểu rõ hơn về các khái niệm và công thức liên quan đến đạo hàm.
Đạo hàm có rất nhiều ứng dụng trong thực tế, chẳng hạn như:
Việc hiểu rõ về đạo hàm không chỉ giúp học sinh giải các bài tập trong chương trình học mà còn mở ra nhiều cơ hội ứng dụng trong các lĩnh vực khác nhau của cuộc sống.
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ tự tin giải Bài 2 trang 126 SGK Toán 11 tập 1 - Chân trời sáng tạo và các bài tập tương tự. Chúc các em học tốt!