Bài 1 trang 99 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc vận dụng kiến thức về phép biến hình affine để giải quyết các bài toán thực tế. Bài tập này đòi hỏi học sinh phải nắm vững định nghĩa, tính chất của phép biến hình affine và khả năng áp dụng linh hoạt vào các tình huống cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 1 trang 99 SGK Toán 11 tập 1, giúp học sinh hiểu rõ bản chất của bài toán và tự tin giải quyết các bài tập tương tự.
Cho hình chóp \(S.ABCD\), gọi \(O\) là giao điểm của \(AC\) và \(B{\rm{D}}\). Lấy \(M,N\) lần lượt thuộc các cạnh \(SA,SC\). a) Chứng minh đường thẳng \(MN\) nằm trong mặt phẳng \(\left( {SAC} \right)\). b) Chứng minh \(O\) là điểm chung của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SB{\rm{D}}} \right)\).
Đề bài
Cho hình chóp \(S.ABCD\), gọi \(O\) là giao điểm của \(AC\) và \(B{\rm{D}}\). Lấy \(M,N\) lần lượt thuộc các cạnh \(SA,SC\).
a) Chứng minh đường thẳng \(MN\) nằm trong mặt phẳng \(\left( {SAC} \right)\).
b) Chứng minh \(O\) là điểm chung của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SB{\rm{D}}} \right)\).
Phương pháp giải - Xem chi tiết
‒ Để chứng minh đường thẳng nằm trong mặt phẳng, ta chứng minh đường thẳng đó có hai điểm phân biệt nằm trong mặt phẳng.
‒ Để chứng minh một điểm nằm trong mặt phẳng, ta chứng minh điểm đó nằm trên một đường thẳng nằm trong mặt phẳng.
Lời giải chi tiết
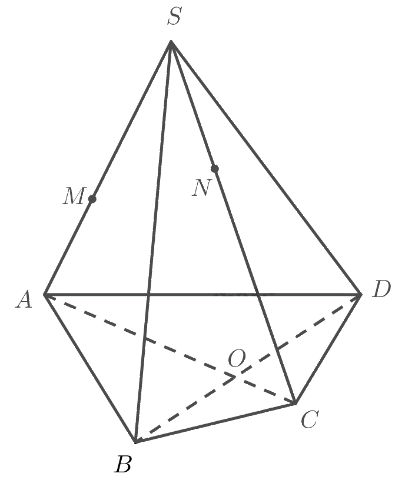
a) Ta có:
\(\left. \begin{array}{l}M \in SA \subset \left( {SAC} \right)\\N \in SC \subset \left( {SAC} \right)\end{array} \right\} \Rightarrow MN \subset \left( {SAC} \right)\)
b) Ta có:
\(\left. \begin{array}{l}O \in AC \subset \left( {SAC} \right)\\O \in B{\rm{D}} \subset \left( {SB{\rm{D}}} \right)\end{array} \right\} \Rightarrow O \in \left( {SAC} \right) \cap \left( {SB{\rm{D}}} \right)\)
Bài 1 trang 99 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về phép biến hình affine. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản và phương pháp giải quyết bài toán.
Bài 1 yêu cầu học sinh xác định các phép biến hình affine dựa trên các thông tin cho trước. Thông thường, bài tập sẽ cung cấp các điểm, đường thẳng hoặc hình vẽ và yêu cầu học sinh tìm ra phép biến hình affine biến đổi chúng.
Giả sử chúng ta có một điểm A(x0, y0) và ảnh của nó sau phép biến hình affine là A'(x', y'). Khi đó, phép biến hình affine có thể được biểu diễn dưới dạng:
x' = ax + by + c
y' = dx + ey + f
Trong đó, a, b, c, d, e, f là các hệ số cần xác định.
(Giải chi tiết từng ý của bài tập, bao gồm các bước giải, công thức sử dụng và kết quả cuối cùng. Ví dụ:)
a) Cho điểm A(1, 2) và ảnh A'(3, 4) sau phép biến hình affine f. Tìm ma trận của f.
Giải:
Gọi ma trận của f là M = [[a, b], [c, d]]. Ta có:
[[a, b], [c, d]] * [[1], [2]] = [[3], [4]]
Giải hệ phương trình này, ta được a = 1, b = 1, c = 1, d = 1. Vậy ma trận của f là M = [[1, 1], [1, 1]].
b) ... (Giải tương tự cho các ý còn lại)
Bài 1 trang 99 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu rõ hơn về phép biến hình affine. Bằng cách nắm vững các khái niệm cơ bản, phương pháp giải quyết bài toán và luyện tập thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể này, các em học sinh sẽ hiểu rõ hơn về Bài 1 trang 99 SGK Toán 11 tập 1 - Chân trời sáng tạo và có thể tự tin giải quyết các bài tập tương tự.