Bài 6 trang 41 SGK Toán 11 tập 1 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc giải quyết các bài toán liên quan đến phép biến hóa affine. Bài tập này giúp học sinh củng cố kiến thức về phép biến hóa affine, các tính chất của nó và ứng dụng trong giải toán hình học.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 6 trang 41, giúp các em học sinh nắm vững phương pháp giải và tự tin làm bài tập.
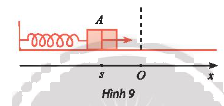
Trong Hình 9, khi được kéo ra khỏi vị trí cân bằng ở điểm O và buông tay, lực đàn hồi của lò xo khiến vật A gắn ở đầu của lò xo dao động quanh O.
Đề bài
Trong Hình 9, khi được kéo ra khỏi vị trí cân bằng ở điểm O và buông tay, lực đàn hồi của lò xo khiến vật A gắn ở đầu của lò xo dao động quanh O. Toạ độ s (cm) của A trên trục Ox vào thời điểm t (giây) sau khi buông tay được xác định bởi công thức \(s = 10sin\left( {10t + \frac{\pi }{2}} \right).\)Vào các thời điểm nào thì \(s = - 5\sqrt 3 \;\)cm?
Phương pháp giải - Xem chi tiết
Phương trình sinx = m ,
Khi đó, tồn tại duy nhất \(\alpha \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\) thoả mãn \(\sin \alpha = m\),
\({\mathop{\rm s}\nolimits} {\rm{inx}} = m \Leftrightarrow \sin x = \sin \alpha \)\( \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Lời giải chi tiết
Khi: \(s = - 5\sqrt 3 \;\)thì \(10sin\left( {10t + \frac{\pi }{2}} \right) = - 5\sqrt 3 \; \Leftrightarrow sin\left( {10t + \frac{\pi }{2}} \right) = - \frac{{\sqrt 3 }}{2}\)
\(\begin{array}{l} \Leftrightarrow sin\left( {10t + \frac{\pi }{2}} \right) = \sin \left( { - \frac{\pi }{3}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}10t + \frac{\pi }{2} = - \frac{\pi }{3} + k2\pi \\10t + \frac{\pi }{2} = \pi + \frac{\pi }{3} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = - \frac{\pi }{{12}} + k\frac{\pi }{5}\\t = \frac{\pi }{{12}} + k\frac{\pi }{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Vậy \(t = \pm \frac{\pi }{{12}} + k\frac{\pi }{5},k \in \mathbb{Z}\) là giá trị cần tìm.
Bài 6 trang 41 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh hiểu sâu hơn về phép biến hóa affine và ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Trước khi đi vào giải bài tập, chúng ta cần nắm vững các khái niệm và tính chất cơ bản của phép biến hóa affine:
Nội dung bài tập: (Giả sử nội dung bài tập được trình bày đầy đủ tại đây. Ví dụ: Cho tam giác ABC. Tìm ảnh của tam giác ABC qua phép biến hóa affine f(x) = Ax + b, với A là ma trận cho trước và b là vector tịnh tiến cho trước.)
Lời giải:
Ví dụ minh họa: (Cung cấp một ví dụ cụ thể với các giá trị A và b cho trước, và giải chi tiết từng bước.)
Để nắm vững kiến thức về phép biến hóa affine và rèn luyện kỹ năng giải bài tập, các em có thể thực hiện các bài tập sau:
Phép biến hóa affine có nhiều ứng dụng trong các lĩnh vực khác nhau, như đồ họa máy tính, xử lý ảnh, và robot học. Các em có thể tìm hiểu thêm về các ứng dụng này để mở rộng kiến thức và hiểu biết của mình.
Kết luận: Bài 6 trang 41 SGK Toán 11 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về phép biến hóa affine. Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trên đây, các em học sinh sẽ nắm vững phương pháp giải và tự tin làm bài tập.