Bài 5 trang 98 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Chân trời sáng tạo, tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số lượng giác, các phép biến đổi lượng giác và giải phương trình lượng giác để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 5 trang 98 SGK Toán 11 tập 2, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Chọn ngẫu nhiên 2 đỉnh của một hình bát giác đều nội tiếp trong đường tròn tâm (O) bán kính (R).
Đề bài
Chọn ngẫu nhiên 2 đỉnh của một hình bát giác đều nội tiếp trong đường tròn tâm \(O\) bán kính \(R\). Xác suất để khoảng cách giữa hai đỉnh đó bằng \(R\sqrt 2 \) là
A. \(\frac{2}{7}\).
B. \(\frac{3}{7}\).
C. \(\frac{4}{7}\).
D. \(\frac{5}{{56}}\).
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính xác suất: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\).
Lời giải chi tiết
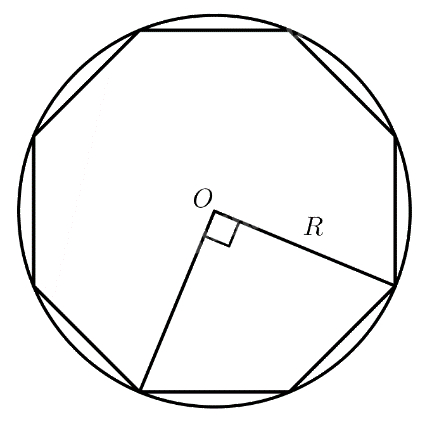
\(A\) là biến cố “Khoảng cách giữa hai đỉnh đó bằng \(R\sqrt 2 \)”
Chọn ngẫu nhiên 2 đỉnh trong tổng số 8 đỉnh có \({C}_8^2 = 28\) cách \( \Rightarrow n\left( \Omega \right) = 28\)
Để khoảng cách 2 đỉnh bằng \(R\sqrt 2 \) thì 2 đỉnh cách nhau 1 đỉnh. Vậy có 8 cách \( \Rightarrow n\left( A \right) = 8\)
\( \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{8}{{28}} = \frac{2}{7}\)
Chọn A.
Bài 5 trang 98 SGK Toán 11 tập 2 Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về hàm số lượng giác và các ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 5 yêu cầu học sinh giải các bài toán liên quan đến việc xác định tập xác định của hàm số lượng giác, tìm giá trị của hàm số tại một điểm, và giải phương trình lượng giác. Các bài toán này thường đòi hỏi học sinh phải nắm vững các công thức lượng giác cơ bản, các phép biến đổi lượng giác, và các phương pháp giải phương trình lượng giác.
Để giải Bài 5 trang 98 SGK Toán 11 tập 2, chúng ta cần thực hiện các bước sau:
Ví dụ 1: Giải phương trình sin(x) = 1/2
Lời giải: Phương trình sin(x) = 1/2 có nghiệm là x = π/6 + k2π và x = 5π/6 + k2π, với k là số nguyên.
Ví dụ 2: Tìm tập xác định của hàm số y = tan(x)
Lời giải: Tập xác định của hàm số y = tan(x) là tất cả các giá trị x sao cho cos(x) ≠ 0, tức là x ≠ π/2 + kπ, với k là số nguyên.
Để hiểu sâu hơn về Bài 5 trang 98 SGK Toán 11 tập 2, học sinh nên:
Khi giải Bài 5 trang 98 SGK Toán 11 tập 2, học sinh cần lưu ý:
Bài 5 trang 98 SGK Toán 11 tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số lượng giác. Bằng cách nắm vững các công thức lượng giác, các phép biến đổi lượng giác, và các phương pháp giải phương trình lượng giác, học sinh có thể tự tin giải quyết các bài toán tương tự.
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về Bài 5 trang 98 SGK Toán 11 tập 2 và đạt kết quả tốt trong học tập.