Bài 11 trang 87 SGK Toán 11 tập 2 thuộc chương trình Toán 11 Chân trời sáng tạo, tập trung vào việc giải quyết các bài toán liên quan đến phép biến hình. Bài tập này giúp học sinh củng cố kiến thức về các phép biến hình cơ bản như phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 11 trang 87, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\)
Đề bài
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\); \(AB = AD = 2a;CD = a\); số đo góc nhị diện \(\left[ {S,BC,A} \right]\) bằng \({60^ \circ }\). Gọi \(I\) là trung điểm của cạnh \(A{\rm{D}}\). Biết hai mặt phẳng \(\left( {SBI} \right)\) và \(\left( {SCD} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Tính thể tích khối chóp \(S.ABCD\) theo \(a\).
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\).
Lời giải chi tiết
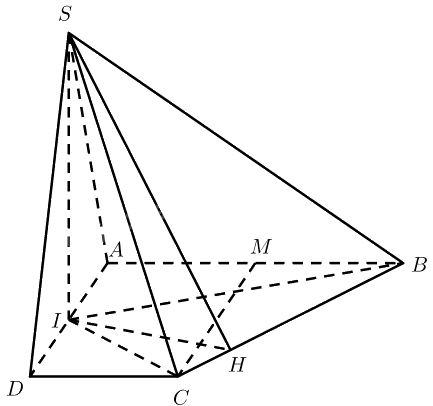
\(\left. \begin{array}{l}\left( {SBI} \right) \bot \left( {ABCD} \right)\\\left( {SCI} \right) \bot \left( {ABCD} \right)\\\left( {SBI} \right) \cap \left( {SCI} \right) = SI\end{array} \right\} \Rightarrow SI \bot \left( {ABCD} \right)\)
Kẻ \(IH \bot BC\left( {H \in BC} \right)\)
\(SI \bot \left( {ABCD} \right) \Rightarrow SI \bot BC\)
\( \Rightarrow BC \bot \left( {SIH} \right) \Rightarrow BC \bot SH\)
Vậy \(\widehat {AHI}\) là góc nhị diện \(\left[ {S,BC,A} \right]\)\( \Rightarrow \widehat {AHI} = {60^ \circ }\)
\(\begin{array}{l}{S_{ABC{\rm{D}}}} = \frac{1}{2}\left( {AB + C{\rm{D}}} \right).A{\rm{D}} = 3{a^2}\\AI = I{\rm{D}} = \frac{1}{2}A{\rm{D}} = a\\{S_{AIB}} = \frac{1}{2}AB.AI = {a^2},{S_{CI{\rm{D}}}} = \frac{1}{2}C{\rm{D}}.I{\rm{D}} = \frac{{{a^2}}}{2}\\ \Rightarrow {S_{BIC}} = {S_{ABC{\rm{D}}}} - {S_{AIB}} - {S_{CI{\rm{D}}}} = \frac{{3{a^2}}}{2}\end{array}\)
Gọi \(M\) là trung điểm của \(AB\)
\(\begin{array}{l} \Rightarrow BM = \frac{1}{2}AB = a,CM = AD = 2a \Rightarrow BC = \sqrt {B{M^2} + C{M^2}} = a\sqrt 5 \\ \Rightarrow IH = \frac{{2{{\rm{S}}_{BIC}}}}{{BC}} = \frac{{3a\sqrt 5 }}{5} \Rightarrow SI = IH.\tan \widehat {SHI} = \frac{{3a\sqrt {15} }}{5}\end{array}\)
\({V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SI = \frac{{3{a^3}\sqrt {15} }}{5}\)
Bài 11 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng trong chương trình học, yêu cầu học sinh vận dụng kiến thức về các phép biến hình để giải quyết các vấn đề thực tế. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Bài 11 yêu cầu học sinh xác định ảnh của một điểm hoặc một hình qua một phép biến hình cho trước. Các phép biến hình thường gặp bao gồm:
Để giải bài tập này, học sinh cần:
Ví dụ: Giả sử bài tập yêu cầu tìm ảnh của điểm A(1; 2) qua phép tịnh tiến theo vector v = (3; -1). Khi đó, ta có:
A' = A + v = (1 + 3; 2 - 1) = (4; 1)
Vậy, ảnh của điểm A qua phép tịnh tiến là A'(4; 1).
Ngoài việc giải bài tập, học sinh cũng nên tìm hiểu thêm về các ứng dụng thực tế của các phép biến hình trong đời sống và các lĩnh vực khác như:
Để củng cố kiến thức, học sinh có thể tự giải thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Một số bài tập gợi ý:
Bài 11 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng giúp học sinh hiểu sâu hơn về các phép biến hình. Bằng cách nắm vững kiến thức và luyện tập thường xuyên, các em học sinh sẽ tự tin giải quyết các bài tập tương tự và ứng dụng kiến thức vào thực tế.
Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về Bài 11 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo và đạt kết quả tốt trong học tập.