Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 2 theo chương trình Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tối ưu nhất.
Mục 4 trang 10, 11 SGK Toán 11 tập 2 tập trung vào các kiến thức quan trọng về... (phần này sẽ được điền đầy đủ trong bài viết descript_end)
Ta biết rằng, (sqrt 2 ) là một số vô tỉ có thể biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn:
Ta biết rằng, \(\sqrt 2 \) là một số vô tỉ có thể biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn: \(\sqrt 2 = 1,414213562...\)
Cũng có thể coi \(\sqrt 2 \) là giới hạn của dãy số hữu tỉ \(\left( {{r_n}} \right)\):
\(1,4;1,41;1,414;1,4142;...\)
Từ đây, ta lập dãy số các luỹ thừa \(\left( {{3^{{r_n}}}} \right)\).
a) Bảng dưới cho biết những số hạng đầu tiên của dãy số \(\left( {{3^{{r_n}}}} \right)\) (làm tròn đến chữ số thập phân thứ chín). Sử dụng máy tính cầm tay, hãy tính số hạng thứ 6 và thứ 7 của dãy số này.

b) Nêu nhận xét về dãy số \(\left( {{3^{{r_n}}}} \right)\).
Phương pháp giải:
Sử dụng máy tính cầm tay để tính.
Lời giải chi tiết:
a) \({r_6} = {3^{1,414213}} = 4,728801466;{r_7} = {3^{1,4142134}} = 4,728803544\).
b) Ta thấy khi \(n \to + \infty \) thì \({3^{{r_n}}} \to {3^{\sqrt 2 }}\).
Sử dụng máy tính cầm tay, tính các luỹ thừa sau đây (làm tròn đến chữ số thập phân thứ sáu):
a) \(1,{2^{1,5}}\);
b) \({10^{\sqrt 3 }}\);
c) \({\left( {0,5} \right)^{ - \frac{2}{3}}}\).
Phương pháp giải:
Sử dụng máy tính cầm tay.
Lời giải chi tiết:
Để làm tròn đến chữ số thập phân thứ 6:

a,

b,
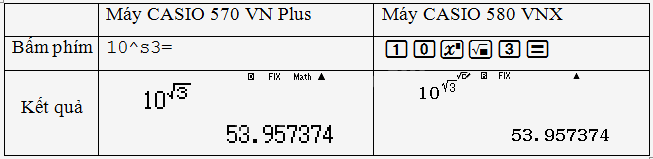
c,

Mục 4 của SGK Toán 11 tập 2 chương trình Chân trời sáng tạo thường xoay quanh các chủ đề về đạo hàm của hàm số, ứng dụng của đạo hàm trong việc khảo sát hàm số và các bài toán liên quan đến cực trị, giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Việc nắm vững kiến thức nền tảng và phương pháp giải là vô cùng quan trọng để đạt kết quả tốt trong các bài kiểm tra và kỳ thi.
Để hiểu rõ hơn về nội dung Mục 4, chúng ta sẽ đi qua từng bài tập cụ thể trong SGK:
Bài tập này yêu cầu học sinh vận dụng các quy tắc tính đạo hàm đã học để tìm đạo hàm của các hàm số đơn giản. Cần chú ý đến quy tắc đạo hàm của tổng, hiệu, tích, thương và đạo hàm của hàm hợp.
Bài tập này yêu cầu học sinh sử dụng quy tắc đạo hàm của tích. Cần nhớ công thức: (uv)' = u'v + uv'.
Lời giải:
Bài tập này yêu cầu học sinh sử dụng quy tắc đạo hàm của hàm hợp. Cần nhớ công thức: (f(g(x)))' = f'(g(x)) * g'(x).
Lời giải:
Đạo hàm đóng vai trò quan trọng trong việc khảo sát hàm số, giúp xác định các điểm cực trị, khoảng đồng biến, nghịch biến và vẽ đồ thị hàm số. Để khảo sát hàm số y = f(x), ta thực hiện các bước sau:
Để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = f(x) trên một khoảng [a, b], ta thực hiện các bước sau:
Việc giải các bài tập trong Mục 4 trang 10, 11 SGK Toán 11 tập 2 Chân trời sáng tạo đòi hỏi sự hiểu biết vững chắc về các khái niệm và quy tắc đạo hàm. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, bạn sẽ tự tin hơn trong việc giải quyết các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm.
| Quy tắc | Công thức |
|---|---|
| Đạo hàm của tổng | (u + v)' = u' + v' |
| Đạo hàm của tích | (uv)' = u'v + uv' |
| Đạo hàm của thương | (u/v)' = (u'v - uv')/v2 |
| Đạo hàm của hàm hợp | (f(g(x)))' = f'(g(x)) * g'(x) |