Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11 tập 1 Chân trời sáng tạo. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, tự tin giải quyết các bài tập và đạt kết quả tốt nhất trong môn Toán.
Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được một cung AB có độ dài đúng bằng R (Hình 9).
Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được một cung AB có độ dài đúng bằng R (Hình 9). Đo và cho biết \(\widehat {AOB}\) có số đo bằng bao nhiêu độ.
Phương pháp giải:
Vẽ đường tròn và xác định góc như phía trên đã học
Lời giải chi tiết:
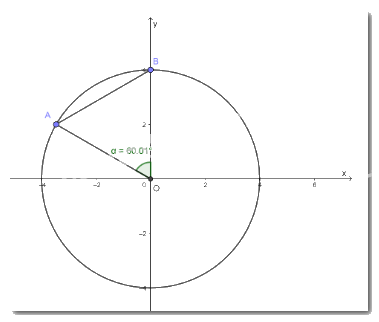
\( \Rightarrow \widehat {AOB} = 60^\circ \)
Hoàn thành bảng chuyển đổi đơn vị đo của các góc sau đây:
Số đo theo độ | 0° | ? | 45° | 60° | ? | 120° | ? | 150° | 180° |
Số đo theo rad | ? | \(\frac{\pi }{6}(rad)\) | ? | ? | \(\frac{\pi }{2}(rad)\) | ? | \(\frac{{3\pi }}{4}(rad)\) | ? | \(\pi (rad)\) |
Phương pháp giải:
Sử dụng công thức \({\alpha ^ \circ } = \frac{{\pi \alpha }}{{180}}\,\)rad ; \(\alpha \,\,rad = {\left( {\frac{{180\alpha }}{\pi }} \right)^0}\)
Lời giải chi tiết:
Số đo theo độ | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° |
Số đo theo rad | 0 | \(\frac{\pi }{6}(rad)\) | \(\frac{\pi }{4}\left( {rad} \right)\) | \(\frac{\pi }{3}\left( {rad} \right)\) | \(\frac{\pi }{2}(rad)\) | \[\frac{{2\pi }}{3}(rad)\] | \(\frac{{3\pi }}{4}(rad)\) | \(\frac{{5\pi }}{6}(rad)\) | \(\pi (rad)\) |
Mục 2 của SGK Toán 11 tập 1 Chân trời sáng tạo tập trung vào các kiến thức cơ bản về giới hạn của hàm số. Đây là một khái niệm quan trọng, nền tảng cho việc học tập các kiến thức nâng cao hơn trong chương trình Toán học. Việc nắm vững các định nghĩa, tính chất và phương pháp tính giới hạn là điều cần thiết để giải quyết các bài tập một cách chính xác và hiệu quả.
Mục 2 bao gồm các nội dung chính sau:
Bài tập này yêu cầu học sinh vận dụng định nghĩa và các tính chất của giới hạn để tính giới hạn của các hàm số đơn giản. Ví dụ:
lim (x→2) (x^2 + 1)
Giải: Thay x = 2 vào hàm số, ta được: 2^2 + 1 = 5. Vậy lim (x→2) (x^2 + 1) = 5.
Bài tập này yêu cầu học sinh tìm giới hạn của hàm số khi x tiến tới vô cùng. Ví dụ:
lim (x→∞) (1/x)
Giải: Khi x tiến tới vô cùng, 1/x tiến tới 0. Vậy lim (x→∞) (1/x) = 0.
Bài tập này yêu cầu học sinh sử dụng định nghĩa của giới hạn để chứng minh một giới hạn cụ thể. Đây là bài tập đòi hỏi sự hiểu biết sâu sắc về định nghĩa và khả năng vận dụng linh hoạt.
Ngoài các bài tập cơ bản, Mục 2 còn xuất hiện các dạng bài tập phức tạp hơn, đòi hỏi học sinh phải có kỹ năng phân tích và giải quyết vấn đề tốt. Một số dạng bài tập thường gặp bao gồm:
Để học tốt Mục 2, bạn nên:
Giải mục 2 trang 9, 10 SGK Toán 11 tập 1 Chân trời sáng tạo là một bước quan trọng trong quá trình học tập môn Toán. Hy vọng rằng với những lời giải chi tiết và hướng dẫn cụ thể trên đây, bạn sẽ tự tin hơn trong việc giải quyết các bài tập và đạt kết quả tốt nhất.