Chào mừng bạn đến với bài học về Lý thuyết Giới hạn của hàm số, một trong những khái niệm quan trọng nhất trong chương trình Toán 11 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn kiến thức cơ bản và nâng cao về giới hạn, giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.
Tại giaitoan.edu.vn, chúng tôi cam kết mang đến cho bạn trải nghiệm học tập trực tuyến tốt nhất với các bài giảng được trình bày rõ ràng, dễ hiểu và đầy đủ.
1. Giới hạn hữu hạn của hàm số tại một điểm
1. Giới hạn hữu hạn của hàm số tại một điểm
Cho khoảng K chứa điểm \({x_0}\)và hàm số \(y = f(x)\) xác định trên K hoặc trên \(K\backslash \left\{ {{x_0}} \right\}\). Ta nói hàm số \(y = f(x)\) có giới hạn hữu hạn là số L khi \(x\) dần tới \({x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì, \({x_n} \in K\backslash \left\{ {{x_0}} \right\}\) và \({x_n} \to {x_0}\), ta có\(f({x_n}) \to L\)
Kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) hay \(f(x) \to L\), khi \({x_n} \to {x_0}\).
2. Các phép toán về giới hạn hữu hạn của hàm số
a, Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) và \(\mathop {\lim }\limits_{x \to {x_0}} g(x) = M\) thì
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x) \pm g(x)} \right] = L \pm M\)
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x).g(x)} \right] = L.M\)
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {\frac{{f(x)}}{{g(x)}}} \right] = \frac{L}{M}\left( {M \ne 0} \right)\)
b, Nếu \(f(x) \ge 0\) với mọi \(x \in \left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}\) và \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) thì \(L \ge 0\)và \(\mathop {\lim }\limits_{x \to {x_0}} \sqrt {f(x)} = \sqrt L \).
* Nhận xét:
\(\begin{array}{l}a,\mathop {\lim }\limits_{x \to {x_0}} {x^k} = {x_0}^k,k \in {\mathbb{Z}^ + }.\\b,\mathop {\lim }\limits_{x \to {x_0}} \left[ {c.f(x)} \right] = c.\mathop {\lim }\limits_{x \to {x_0}} f(x)\end{array}\)
(\(c \in \mathbb{R}\), nếu tồn tại \(\mathop {\lim }\limits_{x \to {x_0}} f(x) \in \mathbb{R}\))
3. Giới hạn một phía
Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {{x_0};b} \right)\).
Ta nói \(y = f(x)\) có giới hạn bên phải là số L khi \(x \to {x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì,\({x_0} < {x_n} < b\) và \({x_n} \to {x_0}\)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = L\).
Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {a;{x_0}} \right)\).
Ta nói \(y = f(x)\)có giới hạn bên phải là số L khi \(x \to {x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\)bất kì,\(a < {x_n} < {x_0}\) và \({x_n} \to {x_0}\)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = L\).
*Chú ý:
4. Giới hạn hữu hạn của hàm số tại vô cực
Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( {a; + \infty } \right)\). Ta nói hàm số \(f(x)\)có giới hạn là số L khi \(x \to + \infty \) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì \({x_n} > a\) và \({x_n} \to + \infty \)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = L\) hay \(f(x) \to L\) khi \(x \to + \infty \).
Cho hàm số \(y = f(x)\) xác định trên khoảng \(\left( { - \infty ;a} \right)\). Ta nói hàm số \(f(x)\) có giới hạn là số L khi \(x \to - \infty \) nếu với dãy số \(\left( {{x_n}} \right)\) bất kì \({x_n} < a\) và \({x_n} \to - \infty \)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to - \infty } f(x) = L\) hay \(f(x) \to L\) khi \(x \to - \infty \).
* Nhận xét:
\(\mathop {\lim }\limits_{x \to \pm \infty } c = c,\)\(\mathop {\lim }\limits_{x \to \pm \infty } (\frac{c}{{{x^k}}}) = 0\)
5. Giới hạn vô cực của hàm số tại một điểm
- Cho hàm số \(y = f(x)\)xác định trên khoảng \(\left( {{x_0};b} \right)\).
Ta nói hàm số \(f(x)\) có giới hạn bên phải là \( + \infty \) khi \(x \to {x_0}\) về bên phải nếu với dãy số \(\left( {{x_n}} \right)\) bất kì thỏa mãn \({x_0} < {x_n} < b\) và \({x_n} \to {x_0}\) ta có \(f({x_n}) \to + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty \)
Ta nói hàm số \(f(x)\) ó giới hạn bên phải là \( - \infty \) khi \(x \to {x_0}\) về bên trái nếu với dãy số \(\left( {{x_n}} \right)\) bất kì thỏa mãn \(a < {x_n} < {x_0}\) và \({x_n} \to {x_0}\) ta có \(f({x_n}) \to + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty \)
Các giới hạn một bên\(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty \), \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \) được định nghĩa tương tự.
* Chú ý:
Nếu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = L \ne 0\) và \(\mathop {\lim }\limits_{x \to {x_0}^ + } g(x) = + \infty \)hoặc \(\mathop {\lim }\limits_{x \to {x_0}^ + } g(x) = - \infty \)thì \(\mathop {\lim }\limits_{x \to {x_0}^ + } \left[ {f(x).g(x)} \right]\) được tính như sau:

Các quy tắc trên vẫn đúng khi thay \({x_0}^ + \)thành \({x_0}^ - \)(hoặc \( + \infty \),\( - \infty \))
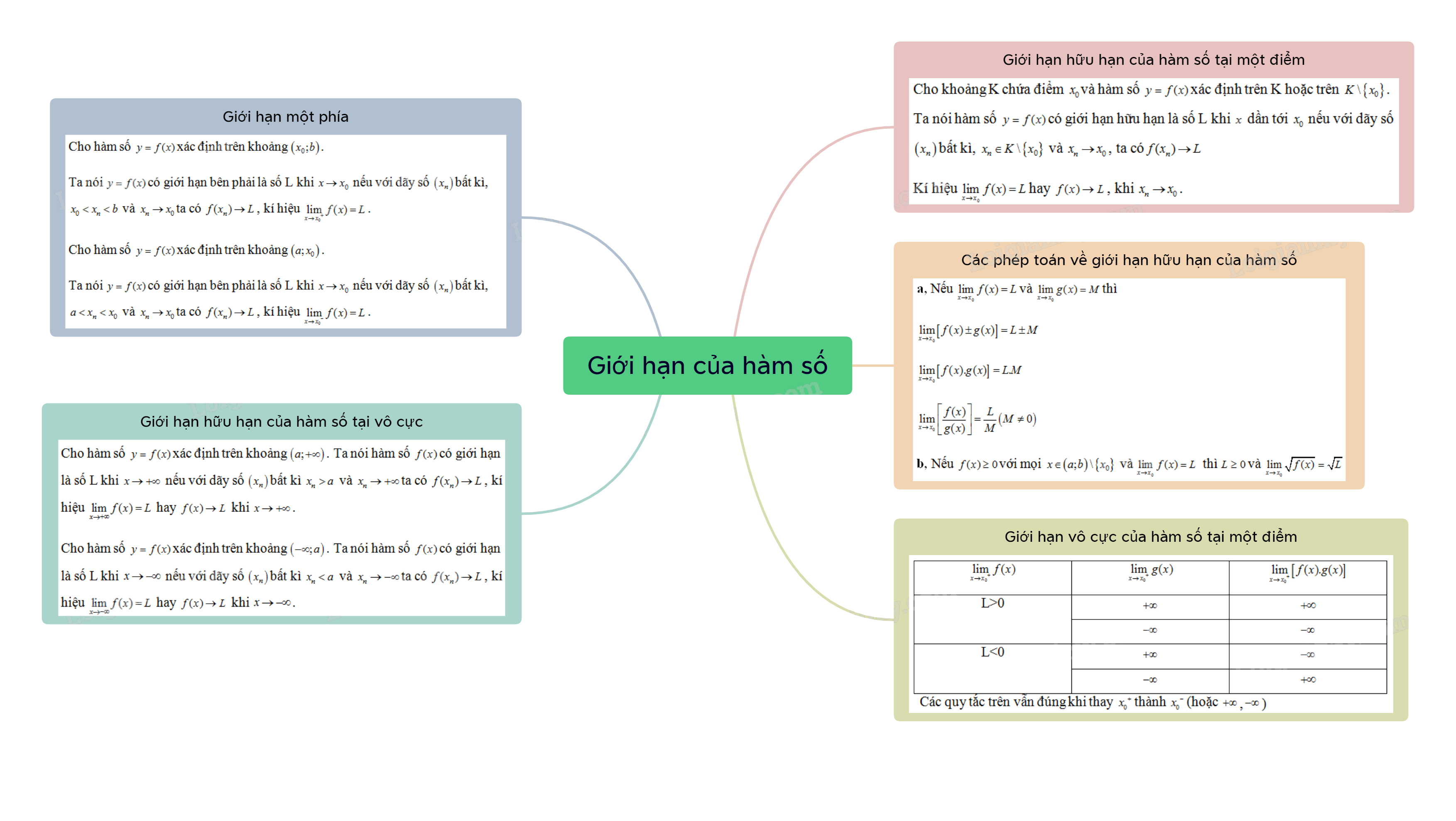
Giới hạn của hàm số là một khái niệm nền tảng trong giải tích, đóng vai trò quan trọng trong việc nghiên cứu sự biến đổi của hàm số khi biến số tiến tới một giá trị nhất định. Trong chương trình Toán 11 Chân trời sáng tạo, học sinh sẽ được làm quen với khái niệm này thông qua các bài học và bài tập thực hành.
Giới hạn của hàm số f(x) khi x tiến tới a, ký hiệu là limx→a f(x), là giá trị mà f(x) tiến tới khi x tiến gần a nhưng không bằng a. Nói cách khác, khi x càng gần a, f(x) càng gần một giá trị L nào đó. Giá trị L được gọi là giới hạn của f(x) khi x tiến tới a.
Ngoài giới hạn hữu hạn, còn có các dạng giới hạn vô cùng, bao gồm:
Việc tính toán giới hạn thường dựa trên các tính chất sau:
Có nhiều phương pháp để tính giới hạn, bao gồm:
Ví dụ 1: Tính limx→2 (x2 - 4) / (x - 2)
Giải: Ta có (x2 - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2) = x + 2 (với x ≠ 2). Do đó, limx→2 (x2 - 4) / (x - 2) = limx→2 (x + 2) = 4.
Ví dụ 2: Tính limx→∞ (2x + 1) / (x - 3)
Giải: Chia cả tử và mẫu cho x, ta được limx→∞ (2 + 1/x) / (1 - 3/x) = (2 + 0) / (1 - 0) = 2.
Khái niệm giới hạn có nhiều ứng dụng trong toán học và các lĩnh vực khác, bao gồm:
Để củng cố kiến thức về giới hạn, bạn có thể thực hành giải các bài tập sau:
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết giới hạn của hàm số. Chúc bạn học tập tốt!