Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 1 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 71 và 72 sách giáo khoa Toán 11 tập 1, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong quá trình học tập.
Xét hàm số \(y = f\left( x \right) = \frac{{2{x^2} - 2}}{{x - 1}}\).
Xét hàm số \(y = f\left( x \right) = \frac{{2{x^2} - 2}}{{x - 1}}\).
a) Bảng sau đây cho biết giá trị của hàm số tại một số điểm gần điểm 1.

Có nhận xét gì về giá trị của hàm số khi \(x\) càng gần đến 1?
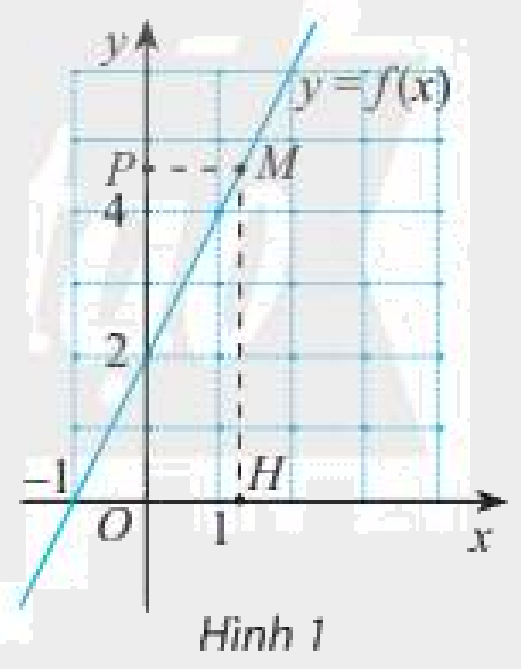
b) Ở Hình 1, \(M\) là điểm trên đồ thị hàm số \(y = f\left( x \right)\); \(H\) và \(P\) lần lượt là hình chiếu của điểm \(M\) trên trục hoành và trục tung. Khi điểm \(H\) thay đổi gần về điểm \(\left( {1;0} \right)\) trên trục hoành thì điểm \(P\) thay đổi như thế nào?
Phương pháp giải:
Quan sát đồ thị và nhận xét.
Lời giải chi tiết:
a) Khi \(x\) càng gần đến 1 thì giá trị của hàm số càng gần đến 4.
b) Khi điểm \(H\) thay đổi gần về điểm \(\left( {1;0} \right)\) trên trục hoành thì điểm \(P\) càng gần đến điểm \(\left( {0;4} \right)\).
Tính các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to 3} \left( {2{x^2} - x} \right)\);
b) \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} + 2x + 1}}{{x + 1}}\).
Phương pháp giải:
Đưa về tính giới hạn của dãy số \(\left( {{x_n}} \right)\) thỏa mãn \({x_n} \to {x_0}\) khi \(n \to + \infty \).
Lời giải chi tiết:
a) Đặt \(f\left( x \right) = 2{x^2} - x\).
Hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\).
Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \({x_n} \to 3\) khi \(n \to + \infty \). Ta có:
\(\lim f\left( {{x_n}} \right) = \lim \left( {2x_n^2 - {x_n}} \right) = 2.\lim x_n^2 - \lim {x_n} = {2.3^2} - 3 = 15\).
Vậy \(\mathop {\lim }\limits_{x \to 3} \left( {2{x^2} - x} \right) = 15\).
b) Đặt \(f\left( x \right) = \frac{{{x^2} + 2x + 1}}{{x + 1}}\).
Hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\).
Giả sử \(\left( {{x_n}} \right)\) là dãy số bất kì thỏa mãn \({x_n} \to - 1\) khi \(n \to + \infty \). Ta có:
\(\lim f\left( {{x_n}} \right) = \lim \frac{{x_n^2 + 2{x_n} + 1}}{{{x_n} + 1}} = \lim \frac{{{{\left( {{x_n} + 1} \right)}^2}}}{{{x_n} + 1}} = \lim \left( {{x_n} + 1} \right) = \lim {x_n} + 1 = - 1 + 1 = 0\).
Vậy \(\mathop {\lim }\limits_{x \to - 1} \frac{{{x^2} + 2x + 1}}{{x + 1}} = 0\).
Mục 1 của chương trình Toán 11 tập 1, Chân trời sáng tạo tập trung vào việc giới thiệu về Hàm số và đồ thị. Đây là một trong những chủ đề quan trọng, đặt nền móng cho các kiến thức toán học nâng cao hơn. Việc hiểu rõ các khái niệm, tính chất của hàm số và cách vẽ đồ thị là vô cùng cần thiết.
Mục 1 bao gồm các nội dung chính sau:
Để giải tốt các bài tập trong Mục 1, các em cần nắm vững các kiến thức sau:
Nội dung: Xác định xem các hàm số sau có phải là hàm số bậc nhất hay không?
Lời giải: Để xác định một hàm số có phải là hàm số bậc nhất hay không, ta cần kiểm tra xem nó có dạng y = ax + b (với a ≠ 0) hay không. Nếu có, thì đó là hàm số bậc nhất. Ngược lại, thì không.
(Giải chi tiết từng hàm số cụ thể ở đây, ví dụ: Hàm số y = 2x + 1 là hàm số bậc nhất vì a = 2 ≠ 0.)
Nội dung: Vẽ đồ thị của hàm số y = -x + 3.
Lời giải: Để vẽ đồ thị của hàm số y = -x + 3, ta thực hiện các bước sau:
(Cung cấp hình ảnh minh họa đồ thị hàm số)
Nội dung: Tìm giao điểm của hai đường thẳng y = x - 2 và y = -2x + 1.
Lời giải: Để tìm giao điểm của hai đường thẳng, ta giải hệ phương trình:
y = x - 2
y = -2x + 1
Thay y = x - 2 vào phương trình thứ hai, ta được: x - 2 = -2x + 1. Giải phương trình này, ta được x = 1. Thay x = 1 vào phương trình y = x - 2, ta được y = -1. Vậy giao điểm của hai đường thẳng là (1; -1).
Trong quá trình giải bài tập, các em cần chú ý:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trên đây, các em sẽ tự tin hơn trong việc học tập môn Toán 11. Chúc các em học tốt!