Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục 4 trang 68 SGK Toán 11 tập 1 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
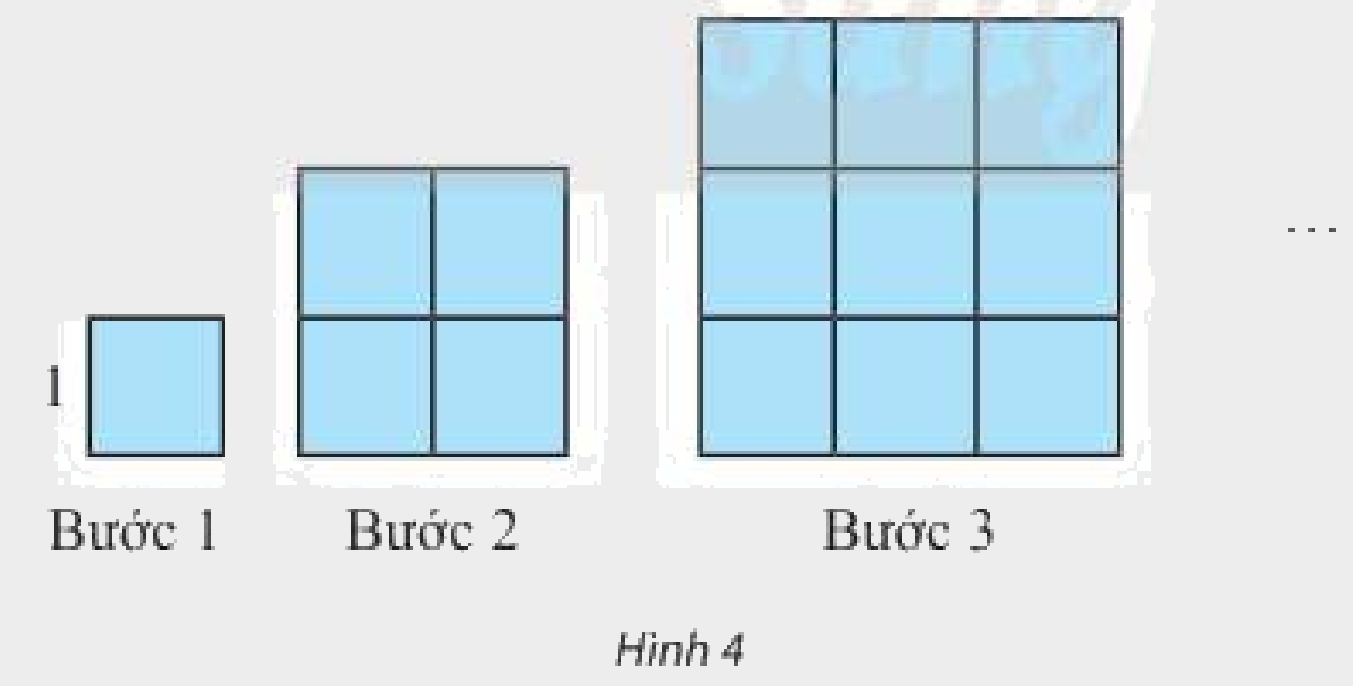
Dựng một dãy hình vuông bằng cách ghép từ các hình vuông đơn vị (cạnh bằng 1 đơn vị độ dài) theo các bước như Hình 4. Kí hiệu ({u_n}) (đơn vị diện tích) là diện tích hình vuông dựng được ở bước thứ (n).
Dựng một dãy hình vuông bằng cách ghép từ các hình vuông đơn vị (cạnh bằng 1 đơn vị độ dài) theo các bước như Hình 4. Kí hiệu \({u_n}\) (đơn vị diện tích) là diện tích hình vuông dựng được ở bước thứ \(n\).
a) Với \(n\) như thế nào thì \({u_n}\) vượt quá 10000; 1000000?
b) Cho hình có diện tích \(S\). Với \(n\) như thế nào thì \({u_n}\) vượt quá \(S\)?
Phương pháp giải:
a) Tìm công thức tổng quát của \({u_n}\) sau đó giải bất phương trình \({u_n} > 10000,{u_n} > 1000000\).
b) Giải bất phương trình \({u_n} > S\).
Lời giải chi tiết:
a) Ta có: \({u_1} = {1^2};{u_2} = {2^2};{u_3} = {3^2};...;{u_n} = {n^2}\)
\(\begin{array}{l}{u_n} > 10000 \Leftrightarrow {n^2} > 10000 = {100^2} \Leftrightarrow n > 100\\{u_n} > 1000000 \Leftrightarrow {n^2} > 1000000 = {1000^2} \Leftrightarrow n > 1000\end{array}\)
b) \({u_n} > S \Leftrightarrow {n^2} > S \Leftrightarrow n > \sqrt S \).
Vậy với các số tự nhiên \(n > \sqrt S \) thì \({u_n} > S\).
Mục 4 trang 68 SGK Toán 11 tập 1 - Chân trời sáng tạo tập trung vào việc ứng dụng kiến thức về hàm số bậc hai để giải quyết các bài toán thực tế. Các bài tập trong mục này thường yêu cầu học sinh xác định các yếu tố của hàm số, vẽ đồ thị hàm số và tìm các điểm đặc biệt của đồ thị như đỉnh, trục đối xứng, giao điểm với các trục tọa độ. Việc nắm vững các kiến thức này là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên.
Mục 4 bao gồm một số bài tập với mức độ khó tăng dần. Dưới đây là phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh xác định hệ số a, b, c của hàm số bậc hai, đỉnh của parabol, trục đối xứng và giao điểm với các trục tọa độ. Để giải bài tập này, học sinh cần nắm vững công thức tính đỉnh, trục đối xứng và giao điểm của parabol.
Bài tập này yêu cầu học sinh vẽ đồ thị của hàm số bậc hai. Để vẽ đồ thị, học sinh cần xác định các yếu tố của hàm số như đỉnh, trục đối xứng, giao điểm với các trục tọa độ và một vài điểm khác trên đồ thị. Sau đó, học sinh kết nối các điểm này lại với nhau để tạo thành parabol.
Bài tập này yêu cầu học sinh tìm giá trị lớn nhất hoặc giá trị nhỏ nhất của hàm số bậc hai. Để giải bài tập này, học sinh cần xét dấu của hệ số a. Nếu a > 0 thì hàm số có giá trị nhỏ nhất tại đỉnh của parabol, và nếu a < 0 thì hàm số có giá trị lớn nhất tại đỉnh của parabol.
Bài tập này yêu cầu học sinh giải phương trình bậc hai bằng đồ thị. Để giải bài tập này, học sinh cần vẽ đồ thị của hàm số bậc hai và tìm các giao điểm của đồ thị với trục hoành. Hoành độ của các giao điểm là nghiệm của phương trình bậc hai.
Để giải các bài tập trong mục 4 trang 68 SGK Toán 11 tập 1 - Chân trời sáng tạo một cách hiệu quả, học sinh cần:
Ví dụ: Giải phương trình 2x2 - 5x + 2 = 0 bằng đồ thị.
Giải:
Giải mục 4 trang 68 SGK Toán 11 tập 1 - Chân trời sáng tạo đòi hỏi học sinh phải nắm vững kiến thức về hàm số bậc hai và rèn luyện kỹ năng giải toán thường xuyên. Hy vọng với những hướng dẫn chi tiết và ví dụ minh họa trên, các bạn học sinh sẽ tự tin hơn trong việc giải quyết các bài tập trong mục này. Chúc các bạn học tốt!