Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho mục 2 trang 39 và 40 sách giáo khoa Toán 11 tập 2, chương trình Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, hiểu rõ phương pháp giải bài tập và tự tin hơn trong quá trình học tập.
Cho hàm số (y = fleft( x right) = frac{1}{2}{x^2}) có đồ thị (left( C right))
Cho hàm số \(y = f\left( x \right) = \frac{1}{2}{x^2}\) có đồ thị \(\left( C \right)\) và điểm \(M\left( {1;\frac{1}{2}} \right)\) thuộc \(\left( C \right)\).
a) Vẽ \(\left( C \right)\) và tính \(f'\left( 1 \right)\).
b) Vẽ đường thẳng \(d\) đi qua điểm \(M\) và có hệ số góc bằng \(f'\left( 1 \right)\). Nêu nhận xét về vị trí tương đối giữa \(d\) và \(\left( C \right)\).
Phương pháp giải:
a) Tính giới hạn \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\).
b) Phương trình đường thẳng đi qua điểm \(A\left( {{x_0};{y_0}} \right)\) có hệ số góc \(k\) là: \(y - {y_0} = k\left( {x - {x_0}} \right)\).
Lời giải chi tiết:
a)
\(\begin{array}{l}f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}{x^2} - \frac{1}{2}}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}\left( {{x^2} - 1} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}\left( {x - 1} \right)\left( {x + 1} \right)}}{{x - 1}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{1}{2}\left( {x + 1} \right) = \frac{1}{2}\left( {1 + 1} \right) = 1\end{array}\)
b) Phương trình đường thẳng \(d\) đi qua điểm \(M\left( {1;\frac{1}{2}} \right)\) và có hệ số góc bằng \(k = f'\left( 1 \right) = 1\) là: \(y - \frac{1}{2} = 1\left( {x - 1} \right) \Leftrightarrow y = x - 1 + \frac{1}{2} \Leftrightarrow y = x - \frac{1}{2}\).
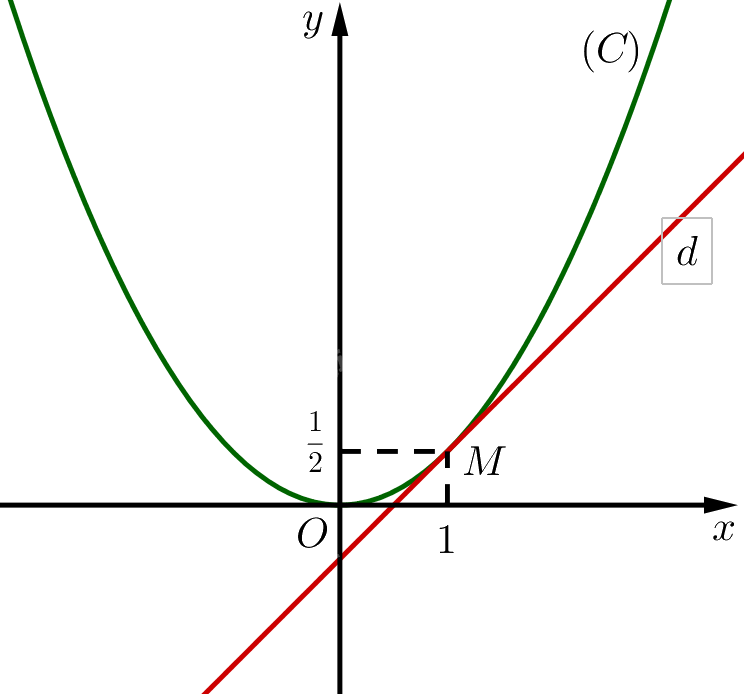
Đường thẳng \(d\) cắt đồ thị hàm số \(\left( C \right)\) tại duy nhất điểm \(M\left( {1;\frac{1}{2}} \right)\).
Cho \(\left( C \right)\) là đồ thị của hàm số \(f\left( x \right) = \frac{1}{x}\) và điểm \(M\left( {1;1} \right) \in \left( C \right)\). Tính hệ số góc của tiếp tuyến của \(\left( C \right)\) tại điểm \(M\) và viết phương trình tiếp tuyến đó.
Phương pháp giải:
Hệ số góc: \(f'\left( {{x_0}} \right)\).
Phương trình tiếp tuyến: \(y - f\left( {{x_0}} \right) = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right)\).
Lời giải chi tiết:
Ta có: \({\left( {\frac{1}{x}} \right)^\prime } = - \frac{1}{{{x^2}}}\) nên tiếp tuyến của \(\left( C \right)\) tại điểm \(M\) có hệ số góc là: \(f'\left( 1 \right) = - \frac{1}{{{1^2}}} = 1\)
Phương trình tiếp tuyến của \(\left( C \right)\) tại điểm \(M\) là: \(y - 1 = 1\left( {x - 1} \right) \Leftrightarrow y = x\).
Mục 2 của chương trình Toán 11 tập 2, Chân trời sáng tạo thường tập trung vào các kiến thức về phép biến hình, bao gồm phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm. Việc nắm vững các phép biến hình này là nền tảng quan trọng để học tập các kiến thức hình học nâng cao hơn trong chương trình.
Các bài tập trong mục 2 trang 39 và 40 thường yêu cầu học sinh:
Bài tập này yêu cầu xác định ảnh của điểm A(x0, y0) qua phép tịnh tiến theo vectơ v = (a, b). Lời giải:
A'(x0 + a, y0 + b)
Để giải bài tập này, học sinh cần hiểu rõ định nghĩa của phép tịnh tiến và cách tìm tọa độ của ảnh sau phép tịnh tiến.
Bài tập này yêu cầu tìm tâm của phép quay biến điểm A thành điểm A'. Lời giải:
Gọi I(x, y) là tâm của phép quay. Khi đó, IA = IA' và góc AIA' bằng góc quay cho trước. Từ đó, ta có thể giải hệ phương trình để tìm tọa độ của điểm I.
Để giải bài tập này, học sinh cần nắm vững các tính chất của phép quay và cách sử dụng hệ phương trình để tìm tọa độ.
Bài tập này yêu cầu chứng minh tam giác ABC là ảnh của tam giác A'B'C' qua phép đối xứng trục. Lời giải:
Chứng minh rằng đường thẳng đi qua trung điểm của hai cạnh tương ứng của hai tam giác là trục đối xứng. Sau đó, chứng minh rằng khoảng cách từ mỗi đỉnh của tam giác ABC đến trục đối xứng bằng khoảng cách từ đỉnh tương ứng của tam giác A'B'C' đến trục đối xứng.
Để giải bài tập này, học sinh cần hiểu rõ các tính chất của phép đối xứng trục và cách chứng minh hai hình đối xứng nhau qua một trục.
Phép biến hình có nhiều ứng dụng trong thực tế, chẳng hạn như:
Hy vọng rằng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập về phép biến hình trong chương trình Toán 11 tập 2, Chân trời sáng tạo. Chúc các em học tập tốt!