Chào mừng các em học sinh đến với lời giải Bài 9 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo. Bài học này tập trung vào việc ôn tập chương 3: Hàm số lượng giác và ứng dụng của hàm số lượng giác.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho hình vuông \(ABCD\) và tam giác đều \(SAB\) cạnh \(a\) nằm trong hai mặt phẳng vuông góc với nhau. Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(AD\).
Đề bài
Cho hình vuông \(ABCD\) và tam giác đều \(SAB\) cạnh \(a\) nằm trong hai mặt phẳng vuông góc với nhau. Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(AD\).
a) Chứng minh rằng \(\left( {SMD} \right) \bot \left( {SNC} \right)\).
b) Tính khoảng cách từ \(M\) đến mặt phẳng \(\left( {SNC} \right)\).
Phương pháp giải - Xem chi tiết
‒ Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng.
‒ Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng.
Lời giải chi tiết
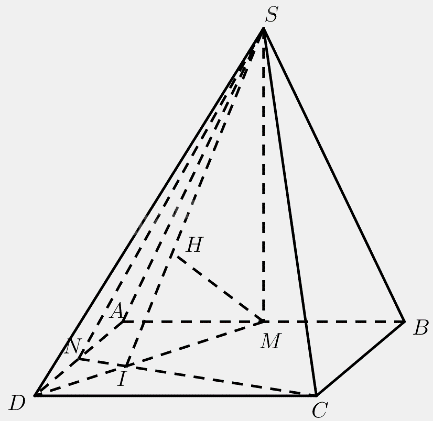
Gọi \(I = CN \cap DM\)
\(\Delta SAB\) đều \( \Rightarrow SM \bot AB\)
Mà \(\left( {SAB} \right) \bot \left( {ABCD} \right),\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\)
\( \Rightarrow SM \bot \left( {ABCD} \right) \Rightarrow SM \bot CN\)
\(\Delta A{\rm{D}}M = \Delta DCN\left( {c.g.c} \right) \Rightarrow \widehat {AM{\rm{D}}} = \widehat {CN{\rm{D}}}\)
Mà \(\widehat {AM{\rm{D}}} + \widehat {A{\rm{D}}M} = {90^ \circ }\)
\(\widehat {CN{\rm{D}}} + \widehat {A{\rm{D}}M} = {90^ \circ } \Rightarrow \widehat {NI{\rm{D}}} = {180^ \circ } - \left( {\widehat {CN{\rm{D}}} + \widehat {A{\rm{D}}M}} \right) = {90^ \circ } \Rightarrow CN \bot DM\)
\(\left. \begin{array}{l}\left. \begin{array}{l}SM \bot CN\\CN \bot DM\end{array} \right\} \Rightarrow CN \bot \left( {SM{\rm{D}}} \right)\\CN \subset \left( {SNC} \right)\end{array} \right\} \Rightarrow \left( {SNC} \right) \bot \left( {SM{\rm{D}}} \right)\)
b) Kẻ \(MH \bot SI\left( {H \in SI} \right)\)
\(CN \bot \left( {SM{\rm{D}}} \right) \Rightarrow CN \bot MH\)
\( \Rightarrow MH \bot \left( {SNC} \right) \Rightarrow d\left( {M,\left( {SNC} \right)} \right) = MH\)
\(\Delta C{\rm{D}}N\) vuông tại \(D\) có đường cao \(DI\)
\(DN = \frac{1}{2}A{\rm{D}} = \frac{a}{2},CN = \sqrt {C{{\rm{D}}^2} + D{N^2}} = \frac{{a\sqrt 5 }}{2},DI = \frac{{C{\rm{D}}.DN}}{{CN}} = \frac{{a\sqrt 5 }}{5}\)
\(DM = CN = \frac{{a\sqrt 5 }}{2} \Rightarrow MI = DM - DI = \frac{{3a\sqrt 5 }}{{10}}\)
\(\Delta SAB\) đều \( \Rightarrow SM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)
\(\Delta SMI\) vuông tại \(M\) có đường cao \(MH\)
\( \Rightarrow MH = \frac{{SM.MI}}{{\sqrt {S{M^2} + M{I^2}} }} = \frac{{3a\sqrt 2 }}{8}\)
Vậy \(d\left( {M,\left( {SNC} \right)} \right) = \frac{{3a\sqrt 2 }}{8}\)
Bài 9 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập tổng hợp, yêu cầu học sinh vận dụng kiến thức đã học trong chương 3 để giải quyết các vấn đề thực tế. Bài tập này bao gồm các dạng câu hỏi khác nhau, từ việc xác định tập xác định của hàm số, tìm tập giá trị, xét tính đơn điệu, đến việc giải phương trình lượng giác và ứng dụng hàm số lượng giác vào các bài toán thực tế.
Bài tập này bao gồm các câu hỏi sau:
Để hàm số y = √(2 - sinx) xác định, điều kiện là 2 - sinx ≥ 0. Vì -1 ≤ sinx ≤ 1, nên 2 - sinx ≥ 2 - 1 = 1 > 0. Vậy, tập xác định của hàm số là R.
Vì -1 ≤ sin2x ≤ 1, nên -3 ≤ 3sin2x ≤ 3. Do đó, -3 + 1 ≤ 3sin2x + 1 ≤ 3 + 1, hay -2 ≤ y ≤ 4. Vậy, tập giá trị của hàm số là [-2, 4].
Hàm số y = cosx có đạo hàm y' = -sinx. Trên khoảng (0, π), sinx > 0, do đó y' < 0. Vậy, hàm số y = cosx nghịch biến trên khoảng (0, π).
Phương trình sin2x = 1/2 tương đương với:
Vậy, nghiệm của phương trình là x = π/12 + kπ và x = 5π/12 + kπ, k ∈ Z.
Gọi h là chiều cao của ngọn hải đăng. Ta có tan60° = h/100. Suy ra h = 100 * tan60° = 100√3 (m). Vậy, chiều cao của ngọn hải đăng là 100√3 mét.
Bài 9 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo là một bài tập quan trọng, giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng với lời giải chi tiết và những lưu ý trên, các em sẽ tự tin giải bài tập này và đạt kết quả tốt trong môn Toán.