Bài 7 trang 86 SGK Toán 11 tập 2 thuộc chương trình học Toán 11 Chân trời sáng tạo. Bài học này tập trung vào việc giải quyết các bài toán liên quan đến đạo hàm của hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập một cách hiệu quả.
Nếu hình hộp chữ nhật có ba kích thước là \(3;4;5\) thì độ dài đường chéo của nó là:
Đề bài
Nếu hình hộp chữ nhật có ba kích thước là \(3;4;5\) thì độ dài đường chéo của nó là:
A. \(5\sqrt 2 \).
B. 50.
C. \(2\sqrt 5 \).
D. 12.
Phương pháp giải - Xem chi tiết
Sử dụng định lí Pitago.
Lời giải chi tiết
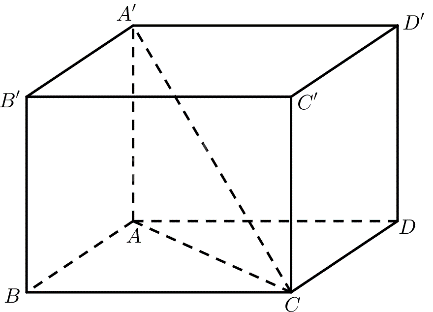
Giả sử hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = 3,BC = 4,AA' = 5\)
\(\begin{array}{l}AC = \sqrt {A{B^2} + B{C^2}} = 5\\A'C = \sqrt {AA{'^2} + A{C^2}} = 5\sqrt 2 \end{array}\)
Chọn A.
Bài 7 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Để giải bài tập này, trước tiên cần nắm vững các khái niệm cơ bản về đạo hàm, bao gồm:
Bài 7 thường bao gồm các dạng bài tập sau:
Phương pháp giải bài tập này thường bao gồm:
Phần 1: Tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1
Để tính đạo hàm của hàm số f(x) = x3 - 3x2 + 2x - 1, ta áp dụng quy tắc đạo hàm của tổng và hiệu, cũng như quy tắc đạo hàm của lũy thừa:
f'(x) = (x3)' - (3x2)' + (2x)' - (1)'
f'(x) = 3x2 - 6x + 2 - 0
f'(x) = 3x2 - 6x + 2
Phần 2: Tìm đạo hàm cấp hai của hàm số g(x) = sin(2x)
Để tìm đạo hàm cấp hai của hàm số g(x) = sin(2x), ta cần tính đạo hàm cấp một trước, sau đó tính đạo hàm của đạo hàm cấp một:
g'(x) = (sin(2x))' = cos(2x) * 2 = 2cos(2x)
g''(x) = (2cos(2x))' = -2sin(2x) * 2 = -4sin(2x)
Ví dụ: Tính đạo hàm của hàm số h(x) = ex + ln(x)
h'(x) = (ex)' + (ln(x))' = ex + 1/x
Bài tập tương tự:
Khi giải bài tập về đạo hàm, cần lưu ý những điều sau:
Đạo hàm có nhiều ứng dụng quan trọng trong thực tế, bao gồm:
Hy vọng với lời giải chi tiết và các ví dụ minh họa trên, các bạn học sinh có thể hiểu rõ hơn về cách giải Bài 7 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo. Chúc các bạn học tập tốt!